Дипломная работа: Сингулярные интегралы

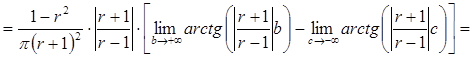
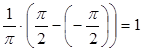при 0<r <1.

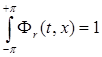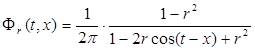Получили, что и - ядро.

2) Докажем, что .

, .

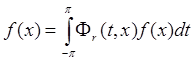Тогда 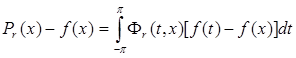. Следовательно достаточно проверить, что .

Найдем такое, что на интервале [x -, x ] ядро возрастает, а на [x , x +] убывает. Это возможно, т. к. производная функции меняет знак с плюса на минус при переходе через точку x : .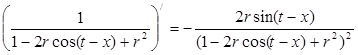

Возьмем ε >0 и найдем такое δ (0<δ <), что при будет 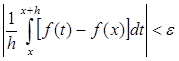, что возможно, так как x есть точка d , т.е. f (t ) в точке t = x есть производная своего неопределенного интеграла.

Тогда по лемме И. П. Натансона

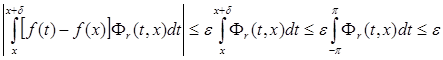, т. к. есть ядро, и .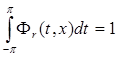

Таким образом, на интервале [x , x +δ ] справедливо неравенство 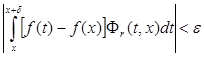. На [x -δ , x ] интеграл рассматривается аналогично в силу симметричности ядра на интервале [x -δ , x +δ ] относительно точки x .

Рассмотрим 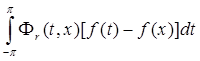за пределами [x -δ , x +δ ], т.е. на

[-π, x - δ , ] и на [x +δ , π ].

В этих случаях выполняются неравенства

, .

Тогда и .

Следовательно , т. к. , и знаменатель дроби не равен нулю.

Аналогично .

То есть на интервалах [-π, x - δ , ] и [x +δ , π ].

При r , достаточно близких к 1, получим

и .

При э