Так как , , то может оказаться и больше, чем . Но это несущественно. Если положим , , то разность между интегралом Фейера (8) и интегралом

при возрастании n стремится к нулю (т. к., например, при будет ), поэтому все рассуждения можно вести для интеграла .

Из (10) и (11) следует, что

.

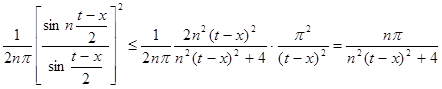Функция есть горбатая мажоранта ядра Фейера.

Но 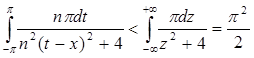, т. е. интегралы от мажоранты ограничены числом, не зависящим от n .

Итак, интеграл Фейера удовлетворяет условиям теоремы

Д. К. Фаддеева. Отсюда следует

Теорема 1 (Л. Фейер – А. Лебег). Почти везде на [- π , + π ] будет

. (12)

Это соотношение выполняется во всех точках Лебега и тем более во всех точках непрерывности функции f (t ), лежащих внутри [- π , + π ].

Тригонометрическая система полна. Это означает, что всякая функция , у которой все коэффициенты Фурье (3) равны нулю, эквивалентна нулю. Избавимся от ограничения, что f (x ) суммируема с квадратом. Справедлива следующая

Теорема 2. Если все коэффициенты Фурье (3) суммируемой функции

f (x ) равны нулю, то f (x ) эквивалентна нулю.

В самом деле, в этом случае и, следовательно, f (x )=0 во всех точках, где имеет место (12), т. е. почти везде.

Теорема 1 позволяет делать некоторые высказывания и о поведении сумм . Для этого заметим, что

,

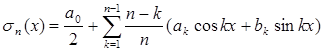так что .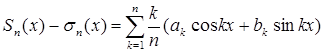

Отсюда .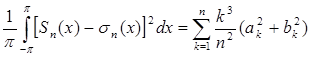

§4. Сингулярный интеграл Пуассона

Пусть точка x есть точка d суммируемой функции f (t ), если в этой точке производная неопределенного интеграла функции f (t ) равна f (x ) (причем ).

Интеграл 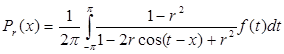(0<r <1) есть сингулярный интеграл Пуассона. Если x (-π <x <π ) есть точка d суммируемой функции f (t ), то (П. Фату).

1) Докажем, что 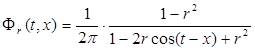- ядро. Т. к. ядро является 2π-периодической функцией, то интеграл от этой функции, рассматриваемый на периоде, не зависит от x . Рассмотрим 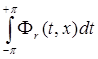при x =0.

.

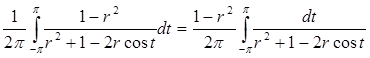Для вычисления интеграла используем универсальную тригонометрическую подстановку и получим

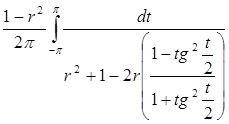. (1)

Обозначим , тогда , а .

Выражение (1) будет равно