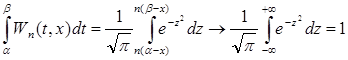.

Эта функция положительна, и она возрастает при и убывает при . Значит, для всякой будет в каждой точке x , где f (t ) есть производная своего неопределенного интеграла.

Определение. Функция Ψ( t , x ) называется горбатой мажорантой функции , если и если Ψ( t , x ) при фиксированном x возрастает на сегменте [ a , x ] и убывает на сегменте [ x , b ] .

Теорема 3 (Д. К. Фаддеев). Если ядро при каждом n имеет такую горбатую мажоранту , что

,

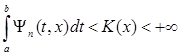где K (x ) зависит лишь от x , то для любой , имеющей точку t = x точкой Лебега, будет справедливо равенство

.

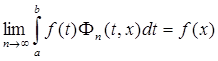Доказательство. Достаточно доказать, что

.

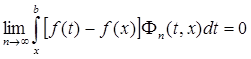Возьмем ε >0 и найдем такое δ >0, что при будет

.

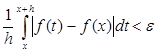По лемме имеем

.

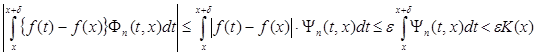С другой стороны, в сегменте [ x + δ , b ] последовательность слабо сходится к нулю, т. к. при будет

.

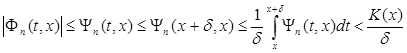Следовательно для достаточно больших n будет

.

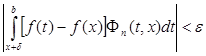При этих n окажется ,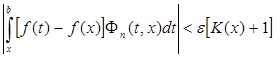

так что 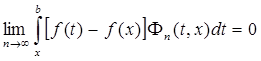. Теорема доказана.

§3. Приложения в теории рядов Фурье

Во введении мы уже определили понятие ряда Фурье функции f (x ) по любой ортонормальной системе . В частности, если речь идет о тригонометрической системе

, (1)

то рядом Фурье функции f (x ) служит ряд

, (2)

где

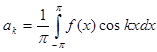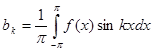, . (3)

Во введении предполагали, что . Это предположение обеспечило существование коэффициентов Фурье функции f (x ) в любой ортонормальной системе. Но функции системы (1) ограничены. Поэтому коэффициенты (3), а с ними и ряд (2), можно образовать для любой суммируемой функции.

Вопрос о сходимости ряда (2) приводится к исследованию некоторого сингулярного интеграла. Если , то, в силу (3), .

Выведем формулу для упрощения выражения в скобках. Для этого сложим равенства

(k =0, 1, …, n -1),