Дипломная работа: Сингулярные интегралы

Интеграл оценивается следующим образом:

.

В интеграле будет , поэтому

,

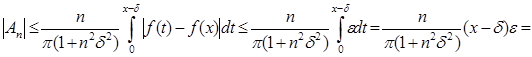
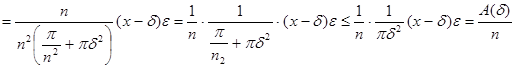где не зависит от n . Аналогично и, следовательно, ,

так что при достаточно больших n будет , т. е. стремится к 0 с возрастанием n , что и требовалось доказать.

Соотношение (3) обеспечивают следующие свойства функции : при больших значениях n те значения , которые отвечают сколько-нибудь заметно удаленным от x значениям t , очень малы, так что величина интеграла (2) определяется в основном значениями подынтегральной функции в непосредственной близости точки x . Но около точки x функция f (t ) почти равна f (x ) (т. к. она непрерывна при t = x ). Значит, если n велико, то интеграл (2) мало изменяется при замене f (t ) на f (x ), т. е. он почти равен интегралу

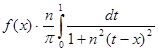
и, в силу (4), почти равен f (x ).

Функция , обладающая подобными свойствами, носит название ядра .

Определение. Пусть функция (n =1, 2, …), заданная в квадрате (, ), суммируема по t при каждом фиксированном x . Она называется ядром , если 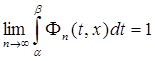при условии, что .

Определение. Интеграл вида 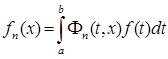, где есть ядро, называется сингулярным интегралом .

В теории сингулярных интегралов очень важен вопрос установления связи предельных значений интеграла при со значением функции

f (t ) в точке x . Так как изменение значения функции f (t ) в одной точке никак не отражается на величине , то необходимо потребовать, чтобы значение f (x ) функции f (t ) в точке x было как-то связано с ее значениями в близких точках. Простейшая форма такой связи есть непрерывность функции f (t ) в точке t = x . Другими формами связи могут служить аппроксимативная непрерывность, требование, чтобы x была точкой Лебега функции f (t ), и т. п.

Теорема 1 (А. Лебег). Пусть на [ a , b ] задана последовательность измеримых функций , , , … Если существует такая постоянная K , что при всех n и t будет

, (5)

и если при всяком c () будет

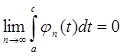, (6)

то, какова бы ни была суммируемая на [ a , b ] функция f (t ), справедливо равенство

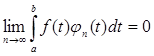. (7)

Доказательство. Если есть сегмент, содержащийся в [ a , b ] , то из (6) следует, что

. (8)

Рассмотрим непрерывную функцию f (t ), и для наперед заданного разложим [ a , b ] точками на столь малые части, чтобы в каждой из них колебание f (t )было меньше, чем ε .

Тогда . (9)

Но , так что первая сумма из (9) не больше, чем Kε ( b - a ). Вторая же сумма (9), в силу (8), стремится к нулю с возрастанием n и для окажется меньшей, чем ε . Для этих n будет

,

так что (7) доказано для непрерывной функции f ( t ).

Пусть f (t )измеримая ограниченная функция .