Дипломная работа: Сингулярные интегралы
И для этих n окажется 
, что и требовалось доказать.
Эта теорема относится к представлению суммируемой функции в точках непрерывности, но суммируемая функция, вообще говоря, не имеет ни одной точки непрерывности, что понижает интерес этой теоремы.
Больший интерес представляет вопрос о представлении суммируемой функции в тех точках, где эта функция служит производной своего неопределенного интеграла, или в точках Лебега, так как и те и другие точки заполняют почти весь сегмент задания функции. Перейдем к рассмотрению этого вопроса.
Лемма (И. П. Натансон). Пусть на сегменте [ a , b ] дана суммируемая функция f (t ), обладающая тем свойством, что
. (1)
Какова бы ни была неотрицательная убывающая функция g (t ), заданная и суммируемая на [ a , b ], интеграл
(2)
существует (может быть как несобственный при t = a ) и справедливо неравенство
. (3)
В пояснение условий леммы заметим, что не исключается случай, когда 
. Если же 
, то функция g (t ) ограничена, и интеграл (2) существует как обычный интеграл Лебега.
Переходя к доказательству леммы, заметим, что не ограничивая общности, можно принять, что g (b )= 0. Действительно, если бы это не было так, то можно было ввести вместо g (t ) функцию g * (t ), определив ее равенствами
g (t ), если 
,
g * (t )=
0, если t=b .
Доказав теорему для g * (t ), мы затем смогли бы всюду заменить g * (t ) на g (t ), т. к. такая замена не отражается на величине интересующих нас интегралов. Итак, считаем, что g (b )=0 .
Пусть a < α < b . На сегменте [ α, b ] функция g (t ) ограничена, и интеграл
(4)
заведомо существует. Если положить 
, то интеграл (4) можно записать в форме интеграла Стилтьеса
,
откуда, после интегрирования по частям, находим
.
Но, в силу (1), мы имеем, что для любого h из интервала [ 0, t -a ] выполняется неравенство 
и следовательно
, (5)
а так как g (t ) убывает, то
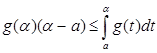. (6)
Значит 
. С другой стороны, функция – g ( t ) возрастает. Отсюда и из (5) следует, что
.
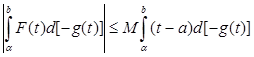Преобразуем стоящий справа интеграл по формуле интегрирования по частям:
.
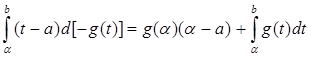