Тогда .

Но .

Интеграл по уже доказанному стремится к нулю и для достаточно больших n становится меньше ε . Значит, для этих n будет

,

что доказывает (7) для случая ограниченной измеримой функции.

Пусть f (t ) произвольная суммируемая функция.

Возьмем ε >0 и, пользуясь абсолютной непрерывностью интеграла, найдем такое δ >0, чтобы для любого измеримого множества с мерой me <δ было .

Сделав это, найдем такую измеримую ограниченную функцию g (t ), чтобы было . Это возможно по

Теореме. Пусть на множестве Е задана измеримая, почти везде конечная функция f (x ). Каково бы ни было ε>0, существует измеримая ограниченная функция g (x ) такая, что .

Можно считать, что на множестве функция g (t ) равна нулю.

Тогда .

Но .

Интеграл же при достаточно больших n будет меньше ε , и при этих n окажется , что и доказывает теорему.

Пример. Пусть . Тогда и . Следовательно выполнены оба условия теоремы Лебега. Аналогично рассматривается случай . Таким образом доказана

Теорема 2 (Риман-Лебег). Для любой суммируемой на [ a , b ] функции

f (t ) будет .

В частности, коэффициенты Фурье , произвольной суммируемой функции стремятся к нулю при .

Если соотношение (7) имеет место для всякой суммируемой на [ a , b ] функции f (t ), то мы будем говорить, что последовательность слабо сходится к нулю .

§2. Представление функции сингулярным интегралом в заданной точке

Во всем дальнейшем будем считать, что ядро при фиксированных n и x ограничено. Тогда сингулярный интеграл 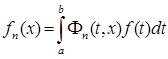имеет смысл при любой суммируемой функции f (t ).

Теорема 1 (А. Лебег). Если при фиксированном x ( a < x < b ) и любом δ>0 ядро слабо сходится к нулю в каждом из промежутков [ a , x - δ ],

[ x + δ , b ] и , где H (x ) не зависит от n , то, какова бы ни была суммируемая функция f (t ), непрерывная в точке x , справедливо равенство

.

Доказательство. Так как есть ядро, то ,

и достаточно обнаружить, что

.

С этой целью, взяв ε >0, найдем такое δ >0, что при будет

.

Это возможно в силу непрерывности функции f в точке x .

Тогда при любом n .