Если, в частности, , то и .

Теорему Н. Н. Лузина можно сформулировать и так: измеримая и почти везде конечная функция становится непрерывной, если пренебречь множеством сколь угодно малой меры.

Определение. Пусть дано измеримое множество E . Взяв произвольную точку x и число h >0, положим E (, h )=E ∙[-h , +h ]. Это тоже измеримое множество.

Предел отношения при h→0 называется плотностью множества E в точке и обозначается через .

Определение. Пусть функция f (x ) задана на сегменте [a , b ] и . Если существует такое измеримое множество E , лежащее на [a , b ] и имеющее точку точкой плотности, что f (x ) вдоль E непрерывна в точке , то говорят, что f (x ) аппроксимативно непрерывна в точке .

Определение. Измеримая функция f (x ) называется функцией с суммируемым квадратом , или функцией, суммируемой с квадратом , если

.

Множество всех функций с суммируемым квадратом обозначается символом .

Определение. Пусть на сегменте [a , b ] задана конечная функция f (x ). Если всякому ε >0 отвечает такое δ >0, что для любой конечной системы взаимно не пересекающихся интервалов , для которой 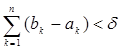оказывается

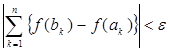, (3)

то говорят, что функция f (x ) абсолютно непрерывна .

Не изменяя смысла определения, можно условие (3) заменить более тяжелым условием .

Определение. Две функции f (x ) и g(x), заданные на сегменте [a , b ], называются взаимно ортогональными , если .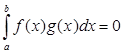

Определение. Функция f (x ), заданная на [a , b ], называется нормальной , если .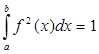

Определение. Система функций , , , …, заданных на сегменте [a , b ], называется ортонормальной системой , если каждая функция системы нормирована, а любые две функции системы взаимно ортогональны.

Определение. Пусть есть ортонормальная система и f (x ) некоторая функция из . Числа 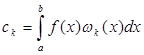называются коэффициентами Фурье функции f (x ) в системе .

Ряд 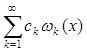называется рядом Фурье функции f (x ) в системе .

§1. Понятие сингулярного интеграла

Чтобы познакомиться с идеей, лежащей в основе понятия сингулярного интеграла, начнем с примера.

Рассмотрим функцию

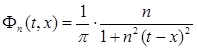. (1)

Если n и x фиксированы, а t меняется от 0 до 1, то эта функция есть непрерывная функция от t . Значит, для всякой суммируемой f (t ) () можно образовать величину

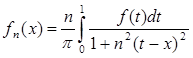. (2)

Докажем, что во всякой точке x (0<x <1), в которой функция f ( t ) непрерывна, будет

. (3)

Для этого прежде всего отметим, что при

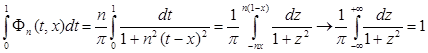. (4)

Поэтому, чтобы установить (3), достаточно показать, что при стремится к нулю разность

.

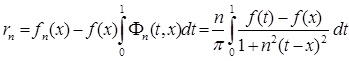Возьмем произвольное и найдем такое , что при будет . Считая, что , представим в форме