Дипломная работа: Сингулярные интегралы

.

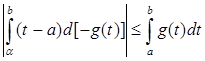Сопоставляя все сказанное, получаем:

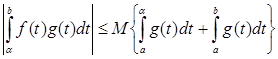. (7)

Хотя это неравенство установлено при предположении, что g (b )= 0, но оно останется верным и без этого предположения. Значит, можно заменить здесь предел b на β , где α< β < b . Но тогда, устремляя α и β к a , получим ,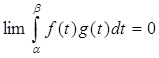

чем доказывается существование интеграла (2). Если в (7) перейти к пределу при , то получим (3). Лемма доказана. (В оценке (3) множителя M уменьшить нельзя, так как при f (t )= 1 в (3) достигается равенство.)

Теорема 2 (П. И. Романовский). Пусть ядро положительно и обладает следующим свойством: при фиксированных n и x ядро , как функция одного лишь t , возрастает в сегменте [ a , x ] и убывает в сегменте

[ x , b ].

Тогда для любой суммируемой функции f (t ), которая в точке x является производной своего неопределенного интеграла, будет .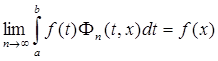

Доказательство. Так как есть ядро, то 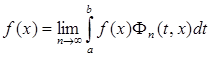и достаточно проверить, что .

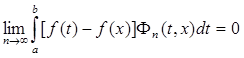Разбивая последний интеграл на два, распространенные на сегменте

[ a , x ] и [ x , b ] , рассмотрим второй из них, так как первый изучается аналогично.

Возьмем ε>0 и найдем такое δ>0 , что при будет

,

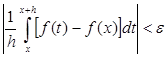что возможно, так как f (t ) в точке t = x есть производная своего неопределенного интеграла. То есть 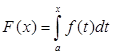и .

Тогда по предыдущей лемме

.

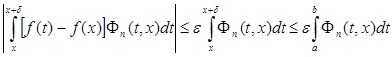Так как есть ядро, то .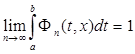

Величина, имеющая конечный предел, ограничена. Значит, существует постоянная K (x ) такая, что .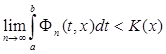

Таким образом,

.

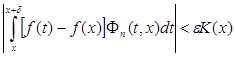С другой стороны, если , то

.

Значит функции на сегменте [ x + δ , b ] равномерно ограничены и выполнено условие (5) теоремы Лебега из §1. Но второе ее условие, т. е. условие (6), также выполнено для этих функций, т. к. является ядром. Следовательно на сегменте [ x + δ , b ] слабо сходится к нулю, и для достаточно больших n будет .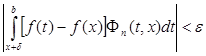

При этих n окажется

,

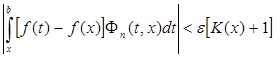так что

.

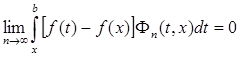Теорема доказана.

В качестве примера ее приложения рассмотрим интеграл Вейерштрасса 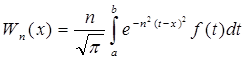.