Дипломная работа: Системы с постоянной четной частью

1) Oтражающая функция

любой системы из рассматриваемого множества совпадает в своей области определения с функцией

2) Любая система вида (1), отражающая функция

которой совпадает в области с функцией содержится в рассматриваемом множестве.

Две системы вида (1), принадлежащие одному классу эквивалентности, будем называть эквивалентными. Допуская определенную вольность речи, будем говорить также, что они имеют одну и ту же отражающую функцию. Функцию при этом будем называть отражающей функцией класса, а класс – соответствующим отражающей функции .

Из третьего свойства отражающей функции следует, что система (1) и система

принадлежат одному классу эквивалентности тогда и только тогда, когда система уравнений

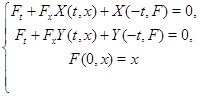
совместна.

Необходимым условием совместности этой системы является тождество .

6. Построение множества систем, четная часть общего решения которых постоянна

6.1 Системы, имеющие постоянную четную часть

Пусть нам дана система

(14)

Перед нами стоит следующий вопрос о том, когда семейство решений этой системы будут иметь постоянную четную часть.

(15)

То есть, когда не будет зависеть от времени .

Возьмем отражающую функцию системы (14) и используя

получим четную часть следующим образом:

(16)

Теорема 15 Если выполнено тождество

где – отражающая функция, для линейной системы вида (14), то любое решение этой системы имеет постоянную четную часть.

Доказательство. Возьмем любое решение системы (14). Его производная

Поэтому можем записать