Дипломная работа: Сравнительный анализ численных методов
но отрезке [а, b], то последовательность ( 3) сходится к единственному корню уравнения ( 2) при любом начальном приближении x0 .
Критерий окончания итерационного процесса. При заданной точности 
>0 вычисления следует вести до тех пор, пока не окажется выполненным неравенство
Если величина 
, то можно использовать более простой критерий окончания итераций:
2.5.2 Решение нелинейного уравнения методом простых итераций
1. Дано уравнение tg (0.36*x +0.4) =x2 . Решить его методом простых итераций с точностью решения
=0,001. Как в предыдущих методах для нахождения корня исследуем функцию
.
Выбираем концы отрезка: a= -1; b = 0. График функции на этом отрезке представлен на рисунке 2.14.
Рисунок 2.14 - График функции на выбранном отрезке
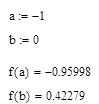
Приведем уравнение к виду x=x- af (x), где итерационная функция (x) =x- af (x), a - итерационный параметр.
Максимальное и минимальное значения производной достигаются на концах отрезка:
Применяем формулу x=x - af (x) =f (x):
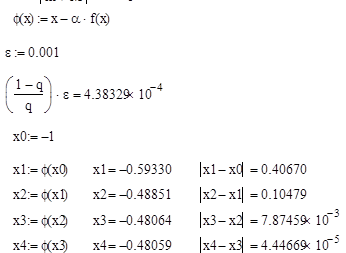
2. Дано уравнение x3 -0,2x2 +0,4x-1,4=0. Решить его методом методом простых итераций с точностью решения=0,001.
Для нахождения корня исследуем функцию 
.
Выбираем концы отрезка: a= -0.1; b = 1.5 График функции на этом отрезке представлен на рисунке 2.15.
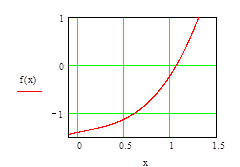
Рисунок 2.15 - График функции на выбранном отрезке.
Найдем корень с помощью встроенной функции root :
Приводим уравнение к виду x= f (x), где