Дипломная работа: Сравнительный анализ численных методов

Проверим условие сходимости:

Максимальное по модулю значение производной итерационной функции достигается в левом конце отрезка:

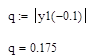
Применяем формулу x=  (x):

2.6 Программа для решения нелинейных уравнений

На рисунках 2.16, 2.17 представлены программы для решения нелинейных уравнений методами хорд и касательных.

Пользователь вводит необходимые данные и при нажатии кнопки "Решить" выводится результат.

Листинги программ представлены в приложениях А, Б.

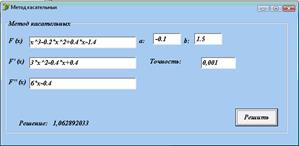
Рисунок 2.16 - Программа для решения методом касательных

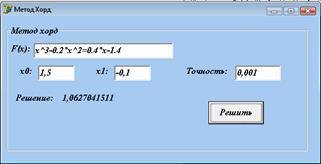
Рисунок 2.17 - Программа для решения методом хорд

3. Решение нелинейных уравнений методом интерполирования

3.1 Интерполяция

Интерполяция является одним из способов аппроксимации функции. Смысл аппроксимации заключается в том, что производится замена одной функции другой в некотором смысле близкой.

Такая задача возникает по многим соображениям в частности, из-за удобства вычисления значений функции, вычисления производных и т.д.

Допустим, в n+1 точке заданы значения x₀ ,x₁ ,…x_n и соответствующие им значения f (x₀ ), f (x₁ ), …, f (x_n ). Значения f (x_i ) вычисляются только в случае, если известна функция f (x), но эти значения могут быть получены, например, экспериментальным путем как значение некой неизвестной функции.

Точки x_i , в которых известны значения функции, носят названия узлов интерполяции .

Интерполяция заключается в выборе функции φ (х), значения которой в узлах интерполяции совпадают со значениями f (x_i ).

φ (х_i ) = f (x_i )

Между узлами значения этих функций могут отличаться (рисунок 3.1).

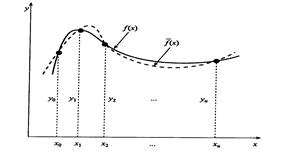
Рисунок 3.1 – Интерполяция

Мы рассмотрим простейший случай, когда в качестве интерполируемой функции используется полином степени n. Преимущества такой интерполяции очевидны. Значения полинома легко вычисляются, имеют непрерывную производную.

3.2 Многочлен Лагранжа

Пусть известны значения некоторой функции f в n+1 различных точках. Возникает задача приближенного восстановления функции f в произвольной точке x. Часто для решения этой задачи строится алгебраический многочлен L_n (x) степени n, который в точках x_i принимает заданные значения, т.е.

L_n (x_i ) =f_i , i=0,1,…,n

и называется интерполяционным.

В частности, мы рассматриваем построение интерполирующего многочлена Лагранжа.

,