Дипломная работа: Старший и верхний центральный показатели линейной системы

где постоянны, содержит лишь одну функцию с наибольшим характеристическим показателем, то

= .

Определение 1.3 [1,с.142]. Система ненулевых вектор-функций

обладает свойством несжимаемости, если характеристичесий показатель любой существенной их линейной комбинации

, ,

где постоянны, совпадает с наибольшим из характеристических показателей комбинируемых вектор-функций, то есть для всякой комбинации y имеем

= .

Определение 1.4 [1,с.137]. Множество всех собственных характеристических показателей (то есть отличных от и ) решений дифференциальной системы будем называть ее спектром.

Теорема 1.1 [1,с.143]. Фундаментальная система линейной системы

,

где и ─ спектр системы , является нормальной тогда и только тогда, когда она обладает свойством несжимаемости.

Замечание 1.2 [1,с.142]. Совокупность вектор-функций с различными характеристическими показателями, очевидно, обладает свойством несжимаемости.

Следствие 1.1 [1,с.145]. Всякая нормальная фундаментальная система реализует весь спектр линейной системы.

Определение1.5 [2,с.71]. Наибольший верхний показатель

системы

будем называть старшим показателем.

Определение 1.6 [2,с.7]. Пусть ─ функция. Тогда верхнее среднее значение функции есть:

= .

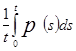Рассмотрим какое-либо семейство кусочно непрерывных и равномерно ограниченных функций:

P = , ,

зависящие от параметра непрерывна в том смысле, что из следует равномерно, по крайней мере, на каждом конечном отрезке .

Определение 1.7 [ 2,с.103]. Ограниченная измеримая функция называется верхней или C-функцией для семейства P, если все функции этого семейства равномерно не превосходят в интегральном смысле функции :

,

то есть, если

,

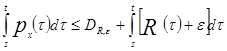где ─ константа, общая для всех и , но, вообще говоря, зависящая от выбора и .