Дипломная работа: Старший и верхний центральный показатели линейной системы

то есть

,

с нормой

, где .

По определению 1.2 найдем для каждой функции ее характеристический показатель Ляпунова, используя определение 1.6:

.

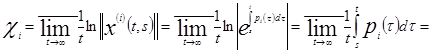
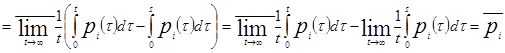Получаем, что

.

Из утверждения 1.3 и определения 1.5 вытекает, что

,

так как матрица конечномерная.

По определению 1.9

_{P ,}

где (P).

3.2 Старший и верхний центральный показатели для диагональной системы с постоянными коэффициентами. Случай .

Исследуем случай, когда матрица системы с постоянными коэффициентами является диагональной. Найдем для нее и .

Рассмотрим диагональную систему

,

где ─ вектор-функция размерности , ─ некоторые числа, .

Она имеет матрицу Коши

,

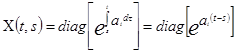то есть

,

с нормой

.

Рассмотрим следующую лемму.

Лемма*.

Пусть ─ некоторое число. Тогда