Дипломная работа: Старший и верхний центральный показатели линейной системы

Во втором случае

.

В третьем случае

.

Найдем нормы :

;

;

.

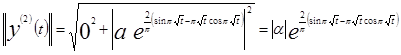Итак,

,

.

В силу определения 1.2:

.

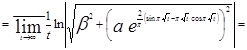
Так как 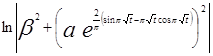─ ограниченная величина, то

А значит, .

;

;

По определению 1.3 следует, что характеристический показатель линейной комбинации совпадает с наибольшим из характеристических показателей комбинируемых решений, то есть

А это означает, что система (1) обладает свойством несжимаемости. Тогда по теореме 1.1 наша фундаментальная система нормальная. По следствию 1.1 вытекает, что реализует весь спектр линейной системы. Значит, спектр системы состоит из одного числа: .

По определению 1.5 старший показатель системы (1) равен нулю, то есть

.

4.2 Вычисление верхнего центрального показателя системы