Дипломная работа: Старший и верхний центральный показатели линейной системы
.
Применительно к нашей системе семейство кусочно непрерывных и равномерно ограниченных функций P состоит из двух функций 
и
, то есть
P
,
где
Для вычисления верхнего центрального показателя 
нам понадобится функция
.
Докажем, что функция 
является верхней для семейства P.
Доказательство:
По определению 1.7 ─ верхняя функция для семейства P, если
.
Докажем, что 
.
.
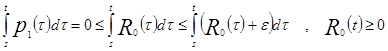Следовательно,
.
Докажем, что 
.
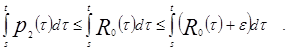
Следовательно,
,
то есть для любого 
Тогда по определению верхней функции
(P) .
Вычислим 
.
По определению 1.6 верхнего среднего значения функции
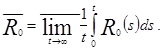
Для всякого 
найдется такое 
, что
.
Тогда