Дипломная работа: Старший и верхний центральный показатели линейной системы

Доказательство.

Так как ,

то

.

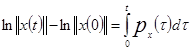Выразим из последнего равенства :

, .

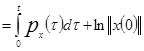Тогда из определения 1.2 следует, что

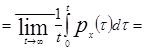[определение 1.6],

то есть

.

Из этого следует, что

.

Так как по определению 1.5

,

то

.

Тогда из следствия 2 получаем, что

.

Так как по определению 1.9

_,

то .

(утверждение 3 доказано)

3 СТАРШИЙ И ВЕРХНИЙ ЦЕНТРАЛЬНЫЙ ПОКАЗАТЕЛИ ДЛЯ ДИАГОНАЛЬНОЙ СИСТЕМЫ

3.1 Старший и верхний центральный показатели для диагональной системы с произвольными коэффициентами

Исследуем случай, когда матрица системы с произвольными коэффициентами является диагональной. Найдем для нее и .

Рассмотрим диагональную систему

,

где ─ вектор-функция размерности . Она имеет матрицу Коши