Изложение: Основные понятия математического анализа

ДВОЙНЫЕ ИНТЕГРАЛЫ

Определение определенного интеграла

- интегральная сумма.

Геометрический смысл ОИ : равен площади криволинейной трапеции.

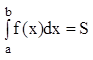
Аналогично ОИ выводится и двойной интеграл.

Пусть задана функция двух переменных z=f(x,y), которая определена в замкнутой области S плоскости ХОУ.

Интегральной суммой для этой функции называется сумма

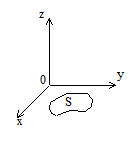
Она распространяется на те значения i и к, для которых точки (x_i ,y_k ) принадлежат области S.

Двойной интеграл от функции z=f(x,y), определенной в замкнутой области S плоскости ХОУ, называется предел соответствующей интегральной суммы.

Правило вычисления двойного интеграла

Двойной интеграл вычисляется через повторные или двукратные интегралы. Различаются два основных вида областей интегрирования.

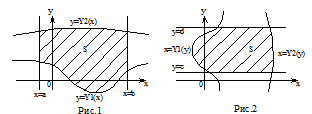
1. (Рис.1) Область интегрирования S ограничена прямыми х=а, х=в и кривыми

.

Для такой области двойной интеграл вычисляется через повторный по формуле:

Сначала вычисляется внутренний интеграл:

При вычислении внутреннего интеграла ‘у’ считается переменной, а ‘х’-постоянной.

2. (Рис.2) Область интегрирования S ограничена прямыми у=С, у=dи кривыми

.

Для такой области двойной интеграл вычисляется через повторный по формуле:

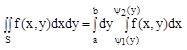
Сначала вычисляется внутренний интеграл, затем внешний.

При вычислении внутреннего интеграла ‘х’ считается переменной, а ‘у’-постоянной.

--> ЧИТАТЬ ПОЛНОСТЬЮ <--