Изложение: Основные понятия математического анализа
Вычисление объемов тел с помощью двойного интеграла
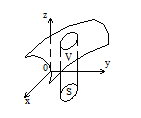
Объем тела, ограниченного сверху поверхностью z=f(x,y), снизу- плоскостью z=0 (плоскость ХОУ) и с боков- цилиндрической поверхностью, вырезающей на плоскости ХОУ область S, вычисляется по формуле:
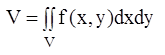
Вычисление площадей поверхностей фигур с помощью двойного интеграла
Если гладкая поверхность задана уравнением z=f(x,y), то площадь поверхности (Sпов.), имеющей своей проекцией на плоскость ХОУ область S, находится по формуле:
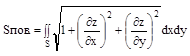- площадь поверхности.
ТРОЙНЫЕ ИНТЕГРАЛЫ
Определяется аналогично двойному интегралу.
Тройной интеграл от функции U=f(x,y,z), распространенным на область V, называется предел соответствующей трехкратной суммы.
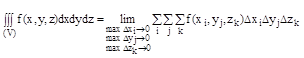
Вычисление тройного интеграла сводится к последовательному вычислению обыкновенных (однократных) нтегралов.
Вычисление объемов тел с помощью тройного интеграла
Объем тела вычисляется по формуле:
НЕСОБСТВЕННЫЕ ИНТЕГРАЛЫ
Это интегралы: - с бесконечными пределами; - от неограниченной функции.
Первый вид
Несобственные интегралы с бесконечными пределами имеют вид:
; 
; 
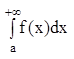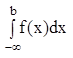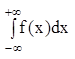
Несобственные интегралы от функции в пределах от (а) до (
) определяются равенством.
1 .
; 2 . 
; 3 . 
Если этот предел существует и конечен, то несобственный интеграл называется сходящимся ; если предел не существует или равен бесконечности, то несобственный интеграл называется расходящимся (ряд сходится или расходится?). Это и есть ответ.
Второй вид
Несобственные интегралы от неограниченной функции имеют вид: 
, где существует точка “с” (точка разрыва) такая, что 
; 
, т.е. 
(в частности c=a; c=b).
Если функция f(x) имеет бесконечный разрыв в точке “с” отрезка [a;b] и непрерывна при 
или 
, то полагаем: 
Если пределы в правой части последнего равенства существуют и конечны, то несобственный интеграл сходится , если пределы не существуют или равны бесконечности - то расходятся .
ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ
1 . Дифференциальное уравнение - уравнение , связывающее независимую переменную х, искомую функцию f(x) и ее производные .