Изложение: Основные понятия математического анализа

Геометрическая прогрессия является сходящимся рядом , если , и расходящимся, если .

Также встречается гармонический ряд (ряд ). Этот ряд расходящийся .

Свойства числовых рядов

1. Если сходится а₁ +а₂ +а₃ +…+а_n +…=, то сходится и ряд а_{m +1} +а_m+2 +а_m+3 +…, полученный из данного ряда отбрасыванием первых m членов. Этот полученный ряд называется m-ым остатком ряда. И, наоборот: из сходимости m-го остатка ряда вытекает сходимость данного ряда. Т.е. сходимость и расходимость ряда не нарушается, если прибавить или отбросить конечное число его членов.

2 . Если ряд а₁ +а₂ +а₃ +… сходится и его сумма равна S, то ряд Са₁ +Са₂ +…, где С= так же сходится и его сумма равна СS.

3. Если ряды а₁ +а₂ +… и b₁ +b₂ +… сходятся и их суммы равны соответственно S1 и S2, то ряды (а₁ +b₁ )+(а₂ +b₂ )+(а₃ +b₃ )+… и (а₁ -b₁ )+(а₂ -b₂ )+(а₃ -b₃ )+… также сходятся. Их суммы соответственно равны S1+S2 и S1-S2.

4. а). Если ряд сходится, то его n-ый член стремится к 0 при неограниченном возрастании n (обратное утверждение неверно).

- необходимый признак (условие) сходимости ряда .

б). Если то ряд расходящийся – достаточное условие расходимости ряда .

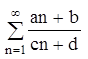-ряды такого вида исследуются только по 4 свойству. Это расходящиеся ряды.

Знакоположительные ряды

Признаки сходимости и расходимости знакоположительных рядов.

Знакоположительные ряды это ряды, все члены которых положительные. Эти признаки сходимости и расходимости мы будем рассматривать для знакоположительных рядов.

1. Первый признак сравнения.

Пусть даны два знакоположительных ряда а₁ +а₂ +а₃ +…+а_n +…=(1) и b₁ +b₂ +b₃ +…+b_n +…=(2).

Если члены ряда (1) не больше соответствующих членов ряда (2), т.е. а_n b_n и ряд (2) сходится , то и ряд (1) также сходится.

Если члены ряда (1) не меньше соответствующих членов ряда (2), т.е. а_n b_n и ряд (2) расходится , то и ряд (1) также расходится.

Этот признак сравнения справедлив, если неравенство выполняется не для всех n, а лишь начиная с некоторого.

2. Второй признак сравнения

Если существует конечный и отличный от нуля предел , то оба ряда сходятся или расходятся одновременно.

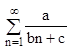-ряды такого вида расходятся по второму признаку сравнения. Их надо сравнивать с гармоническим рядом.

3. Признак Даламбера

Если для знакоположительного ряда (а₁ +а₂ +а₃ +…+а_n +…=) существует (1), то ряд сходится, если q<1, расходится, если q>1. Если q=1 то вопрос остается открытым.

4. Признак Коши радикальный

Если для знакоположительного ряда существует предел (2), то ряд сходится, если q<1, расходится, если q>1. Если q=1 то вопрос остается открытым.

5. Признак Коши интегральный

Вспомним несобственные интегралы.