Изложение: Основные понятия математического анализа

Существуют следующие формы комплексных чисел: алгебраическая (x+iy), тригонометрическая (r(cos+isin)), показательная (reⁱ ).

Всякое комплексное число z=x+iy можно изобразить на плоскости ХОУ в виде точки А(х,у).

Плоскость, на которой изображаются комплексные числа, называется плоскостью комплексного переменного z (на плоскости ставим символ z).

Ось ОХ – действительная ось, т.е. на ней лежат действительные числа. ОУ – мнимая ось с мнимыми числами.

x + iy - алгебраическая форма записи комплексного числа.

Выведем тригонометрическую форму записи комплексного числа.

;

Подставляем полученные значения в начальную форму:

, т.е.

r ( cos + isin ) - тригонометрическая форма записи комплексного числа.

Показательная форма записи комплексного числа следует из формулы Эйлера:

, тогда

z=reⁱ - показательная форма записи комплексного числа.

Действия над комплексными числами

1. сложение. z₁ +z₂ =(x1+iy1)+ (x2+iy2)=(x1+x2)+i(y1+y2);

2 . вычитание. z₁ -z₂ =(x1+iy1)- (x2+iy2)=(x1-x2)+i(y1-y2);

3. умножение. z₁ z₂ =(x1+iy1)*(x2+iy2)=x1x2+i(x1y2+x2y1+iy1y2)=(x1x2-y1y2 )+i(x1y2+x2y1);

4 . деление. z₁ /z₂ =(x1+iy1)/(x2+iy2)=[(x1+iy1)*(x2-iy2)]/[ (x2+iy2)*(x2-iy2)]=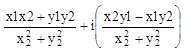

Два комплексных числа, которые отличаются только знаком мнимой единицы, т.е. z=x+iy (z=x-iy), называются сопряженными.

Произведение

- Если комплексные числа заданы в тригонометрической форме.

z1=r(cos+isin); z2=r(cos+isin).

То произведение z1*z2 комплексных чисел находится: , т.е. модуль произведения равен произведению модулей, а аргумент произведения равен сумме аргументов сомножителей.

- Если комплексные числа заданы в показательной форме.

; ;

Частное

- Если комплексные числа заданы в тригонометрической форме.