Книга: Вивчення диференціального числення функцій однієї та багатьох змінних в умовах модульно-рейтингової
Функція ![]() , визначена на проміжку
, визначена на проміжку ![]() , називається парною , якщо для будь-якого
, називається парною , якщо для будь-якого ![]() виконується рівність
виконується рівність
![]()
Графік парної функції симетричний відносно осі ординат.
Функція ![]() , визначена на проміжку
, визначена на проміжку ![]() , називається непарною , якщо для будь-якого
, називається непарною , якщо для будь-якого ![]() виконується рівність
виконується рівність
![]()
Графік непарної функції симетричний відносно початку координат.
Приклад 1. Нехай ![]() , де
, де ![]() . Згідно з відомою властивістю даної функції,
. Згідно з відомою властивістю даної функції,
![]()
Отже, ![]() є непарною функцією.
є непарною функцією.
Приклад 2. Нехай ![]() , де
, де ![]() . Відомо, що
. Відомо, що
![]()
Отже, ![]() є парною функцією.
є парною функцією.
Приклад 3. Дослідити на парність чи непарність функцію
![]()
Знайдемо область визначення функції:
![]()
Знайдемо ![]() :
:
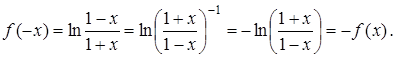
Одержали, що ![]() , тобто
, тобто ![]() — непарна.
— непарна.
Функція ![]() , визначена на всій числовій осі, називається періодичною , якщо існує число
, визначена на всій числовій осі, називається періодичною , якщо існує число ![]() таке, що для всіх
таке, що для всіх ![]() виконується тотожність
виконується тотожність
![]()
Число Т при цьому називається періодом функції ![]() , а саму функцію називають Т -переодічною .
, а саму функцію називають Т -переодічною .
Якщо число Т є періодом функції ![]() , то й число –Т є також періодом
, то й число –Т є також періодом ![]() :
:
![]()
Якщо ![]() — періодична функція з періодом Т, то функція
— періодична функція з періодом Т, то функція ![]() , де
, де ![]() , є періодичною з періодом
, є періодичною з періодом ![]() .
.
Зокрема, якщо розглянути функцію ![]() , де
, де ![]() — сталі, то періодом цієї функції є число
— сталі, то періодом цієї функції є число ![]() .
.
Зауважимо, що функцію ![]() у фізиці називають гармонікою , число
у фізиці називають гармонікою , число ![]() називають амплітудою ,
називають амплітудою , ![]() — циклічною частотою , а
— циклічною частотою , а ![]() — початковою фазою гармоніки .
— початковою фазою гармоніки .
Приклад 4. Знайти період функції ![]() .
.
Розв’язання. Функція ![]() має період
має період ![]() , тому функція
, тому функція ![]() має період
має період ![]() .
.