Книга: Вивчення диференціального числення функцій однієї та багатьох змінних в умовах модульно-рейтингової

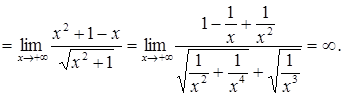
б)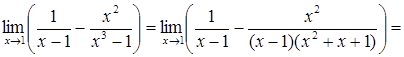

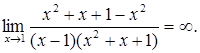
Невизначеність виду

Невизначеність виду розкривається за допомогою другої стандартної границі.

Приклад 6.

а)

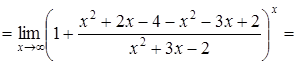
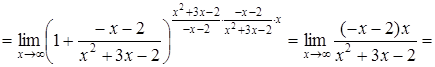
б)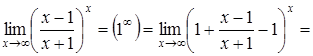

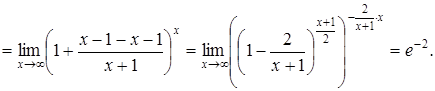
в)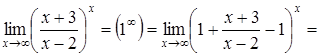

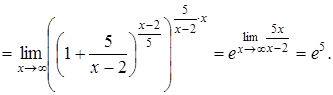
Приклади обчислення границь за допомогою еквівалентних нескінченно малих:

а) .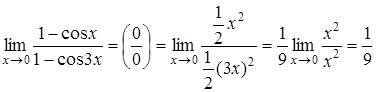

б) .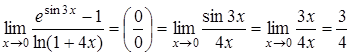

.

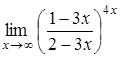1. 5 Неперервність функції. Дослідження функції на неперервність

Функціяназивається неперервною в точці , якщо існує границя функції в цій точці і вона дорівнює значенню функції в точці :

Функція в точці буде неперервною тоді і тільки тоді, коли виконуються умови:

1. функція визначена в околі точки ;

2. існує границя функції в точці ;

3. границя функції дорівнює значенню функції в цій точці, тобто

(1)

Разом усі ці умови є необхідними й достатніми для того, щоб функція була неперервною в точці .

На практиці при дослідженні функцій на неперервність користуються ознаками, які безпосередньо випливають із співвідношення (1), а саме:

для того, щоб функція була неперервною в точці , треба щоб: