Книга: Вивчення диференціального числення функцій однієї та багатьох змінних в умовах модульно-рейтингової

При обчисленні границь найчастіше використовують деякі важливі формули:

— перша важлива границя ;

; — друга важлива границя ,

де е — ірраціональне число, е = 2,718281...

Наслідки з важливих границь

1. 2.

3. 4.

5. 6.

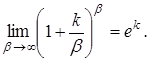
Розкриття невизначеностей

Обчислення границь зводиться до підстановки в даний вираз граничного значення аргументу. Якщо при цьому одержуємо неви-значені вирази вигляду то знаходження границь у цих випадках називається розкриттям невизначеності .

Для розкриття невизначеності, перш ніж перейти до границі, необхідно перетворити даний вираз.

Невизначеність виду

Щоб розкрити невизначеність виду , треба чисельник та знаменник дробу поділити почленно на найвищий степінь змінної.

Приклад 1. Знайти границю:

а) .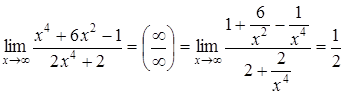

б) .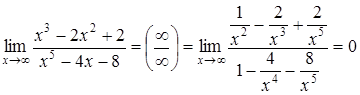

в) .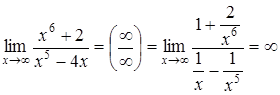

г)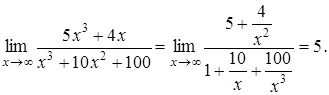

Невизначеність виду

Якщо чисельник та знаменник дробу поліном, що перетворюється в нуль при , для розкриття невизначеності чисельник та знаменник треба поділити на .

Приклад 3. Обчислити:

а) .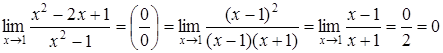

б)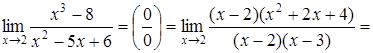

Приклад 4. Знайти границі:

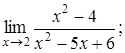
Розв’язання. Безпосередня підстановка числа під знак границі приводить до невизначеності 0/0. Перетворимо вираз, розклавши чисельник і знаменник на множники і скоротивши на :

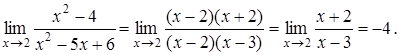
Невизначеність виду

Невизначеність виду перетвореннями приводиться до виду та .

Приклад 5.