Книга: Вивчення диференціального числення функцій однієї та багатьох змінних в умовах модульно-рейтингової
Множина значень ![]() та
та ![]() — проміжок
— проміжок ![]() .
.
Функції ![]() ,
, ![]() ,
, ![]() — непарні, їх графіки симетричні відносно початку координат,
— непарні, їх графіки симетричні відносно початку координат, ![]() — парна, її графік симетричний відносно
— парна, її графік симетричний відносно ![]() .
.
Функції періодичні. Найменший період синуса та косинуса ![]() ,
, ![]() та
та ![]() —
— ![]() .
.
6. Обернені тригонометричні функції
Тригонометричні функції в інтервалі монотонності мають обернені:
![]() — обернена до
— обернена до ![]() на відрізку
на відрізку  ;
;
![]() — обернена до
— обернена до ![]() на відрізку
на відрізку ![]() ;
;
![]() — обернена до
— обернена до ![]() на відрізку
на відрізку 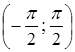 ;
;
![]() — обернена до
— обернена до ![]() на відрізку
на відрізку ![]() .
.
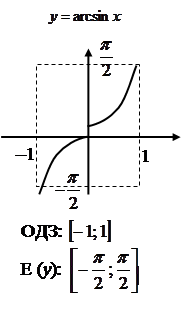 |
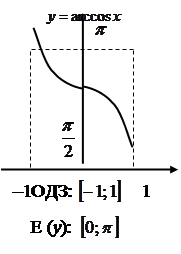 |
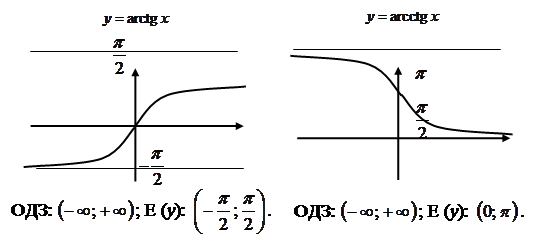
7. Перетворення графіків функцій
При побудові графіків функцій часто використовують дефор-мації та паралельне перенесення вздовж осі ![]() та
та ![]() .
.
Треба знати, що:
1) графік функції ![]() — дзеркальне відображення графіка
— дзеркальне відображення графіка ![]() відносно осі
відносно осі ![]() ;
;
2) графік функції ![]() — дзеркальне відображення графіка
— дзеркальне відображення графіка ![]() відносно осі
відносно осі ![]() ;
;
3) графік функції ![]() , де
, де ![]() — паралельне перенесення графіка
— паралельне перенесення графіка ![]()
 на а одиниць масштабу вздовж осі
на а одиниць масштабу вздовж осі ![]() ;
;
4) графік функції![]() , де
, де ![]() — паралельне перенесення графіка
— паралельне перенесення графіка ![]()
![]() на а одиниць масштабу вздовж осі
на а одиниць масштабу вздовж осі ![]() ;
;
5) графік функції ![]() — стиснення в
— стиснення в ![]() разів
разів ![]() , або розтягнення в
, або розтягнення в ![]() разів
разів ![]() графіка
графіка ![]() вздовж осі
вздовж осі ![]() ;
;
6) графік функції ![]() — розтягнення в
— розтягнення в ![]() разів
разів ![]() , або стиснення в
, або стиснення в ![]() разів
разів![]() , графіка
, графіка ![]() вздовж осі
вздовж осі ![]() ;
;
7) графік функції ![]() — дзеркальне відображення від осі
— дзеркальне відображення від осі ![]() від’ємної частини (під віссю
від’ємної частини (під віссю ![]() ) графіка функції
) графіка функції![]() , додатна частина графіка залишається на місці.
, додатна частина графіка залишається на місці.
8) графік функції ![]() — дзеркальне відображення від осі
— дзеркальне відображення від осі ![]() правої частини (з додатної півплощини) графіка
правої частини (з додатної півплощини) графіка ![]() в ліву півплощину, додатна частина графіка залишається на місці.
в ліву півплощину, додатна частина графіка залишається на місці.
Аналогічно визначаються нескінченно малі й нескінченно великі величини при ![]() .
.
Нескінченно великі величини знаходяться в тісному зв’язку з нескінченно малими: якщо при даному граничному переході функція ![]() є нескінченно великою, то функція
є нескінченно великою, то функція ![]() при цьому самому граничному переході буде нескінченно малою й навпаки.
при цьому самому граничному переході буде нескінченно малою й навпаки.
Властивості нескінченно малих
1. Функцію ![]() можна подати у вигляді
можна подати у вигляді ![]() , де
, де ![]() – стале число;
– стале число; ![]() — нескінченно мала при
— нескінченно мала при ![]() , тоді і тільки тоді, коли
, тоді і тільки тоді, коли ![]() .
.
2. Якщо ![]() , то
, то 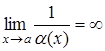 .
.
3. Алгебраїчна сума довільного скінченого числа нескінченно малих функцій є функція нескінченно мала (у самому граничному переході).
4. Добуток нескінченно малої на обмежену функцію є величина нескінченно мала.
5. Добуток скінченого числа нескінченно малих є величина нескінченно мала.
6. Добуток нескінченно малої на постійну є величина нескінченно мала.