Книга: Вивчення диференціального числення функцій однієї та багатьох змінних в умовах модульно-рейтингової
 Розв’язання. В точці
Розв’язання. В точці ![]() функція не визначена. Знайдемо при
функція не визначена. Знайдемо при ![]() границі даної функції зліва та справа:
границі даної функції зліва та справа:


Оскільки односторонні границі скінченні, але
![]() ,
,
то ![]() є точкою розриву першого роду.
є точкою розриву першого роду.
Стрибок в даному випадку в точці ![]() дорівнює 2.
дорівнює 2.
Приклад 2. Дослідити на неперервність функцію ![]()
 Розв’язання. Дана функція визначена у всіх точках за винятком х = 0. Знайдемо односторонні границі функції в цій точці:
Розв’язання. Дана функція визначена у всіх точках за винятком х = 0. Знайдемо односторонні границі функції в цій точці:
![]()
Рівність ![]() означає, що х = 0 є точкою усувного розриву.
означає, що х = 0 є точкою усувного розриву.
Приклад 3. Визначити характер розриву функції

 Розв’язання. Функція в точці
Розв’язання. Функція в точці ![]() не визначена.
не визначена.
При ![]() маємо
маємо ![]() , при
, при ![]()
![]() . Отже,
. Отже, ![]() ,
, ![]() .
.
Тому точка ![]() є точкою розриву другого роду.
є точкою розриву другого роду.
2. Диференціальне числення функції однієї змінної
2.1 Похідна функції в точці ![]()
Похідною функції ![]() в точці х називається границя (як що вона існує) відношення приросту функції
в точці х називається границя (як що вона існує) відношення приросту функції ![]() до приросту аргументу
до приросту аргументу ![]() , коли приріст аргументу прямує до нуля, тобто:
, коли приріст аргументу прямує до нуля, тобто:
![]() . (2.1)
. (2.1)
Функція, яка має скінчену похідну в точці х , називається диференційовною в цій точці. Приріст диференційовної в точці х функції має вигляд
![]() , (2.2)
, (2.2)
де ![]() – нескінченно мала функція при
– нескінченно мала функція при ![]() , тобто диференційовна функція неперервна.
, тобто диференційовна функція неперервна.
Якщо ![]() , тоді функція
, тоді функція ![]() в точці х має нескінченну похідну.
в точці х має нескінченну похідну.
Основні правила диференціювання
![]() (1)
(1)
![]() (2)
(2)
![]() (3)
(3)
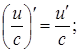 (4)
(4)
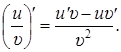 (5)
(5)
Похідні основних елементарних функцій