Контрольная работа: Метод потенциалов для решения транспортной задачи в матричной форме. Задача оптимального распределения ресурсов

t – порядковый номер динамического ряда;

a , b – параметры уравнения.

Задача состоит в определении уровня динамического ряда за пределами взятого базисного периода через определение значений параметров уравнения (a , b ). Базисный период принимается по исходным данным, t _баз = 15.

Параметры модели определяются из соотношений:

; ;

;

,

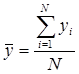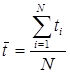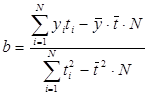где N – число мест базисного периода, N = 15.

Таблица 1 - Характеристики для расчета параметров линейной модели прогноза численности трудовых ресурсов

ti	yi		yi ·ti
1	2	1	2
2	6	4	12
3	10	9	30
4	12	16	48
5	13	25	65
6	17	36	102
7	21	49	147
8	22	64	176
9	25	81	225
10	27	100	270
11	29	121	319
12	30	144	360
13	34	169	442
14	35	196	490
15	38	225	570
120	321	1240	3258

;

а = 21,4 – 2,464 8 = 1,688

Тогда

y = 1,688 + 2,464 t

Для N + 1 года y_{N+ 1} = 41,112.

Ответ: y = 1,688 + 2,464 t

Список использованной литературы

1. Экономико-математическое моделирование. Учеб. для ВУЗов / Под ред. А.Д. Дрогобыцкого. – М.: Экзамен, 2004.

2. Карпелович Ф.И., Садовский Л.Е. Элементы линейной алгебры и линейного программирования. – М.: Физматгиз, 1963.

3. Нестеров Е.П. Транспортные задачи линейного программирования. – М.: Транспорт, 1971.