Контрольная работа: Метод замены неизвестного при решении алгебраических уравнений

Ответ:

Пример 7.

Решение. Обозначим

Таким образом, для и имеем симметричную систему:

Обозначим тогда

Таким образом,

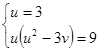
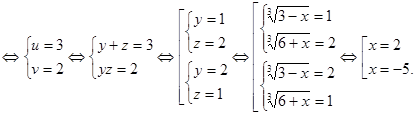
Ответ:

Пример 8.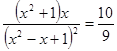

Решение. Можно в этом уравнении освободиться от знаменателя, проделать все необходимые преобразования и убедиться, что получившееся уравнение четвёртой степени является возвратным. Но лучше это сделать быстрее. Поделим числитель и знаменатель дроби, расположенной в левой части, на . Получим

Положим , тогда

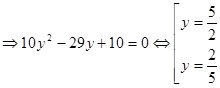
Обратная замена: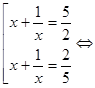

или

корней нет.

Ответ:

Пример 9.

Решение. Так как не является корнем данного уравнения, то, разделив обе его части на , получим уравнение

Сделав замену неизвестной последнее уравнение перепишем в виде

Вернёмся к исходной переменной: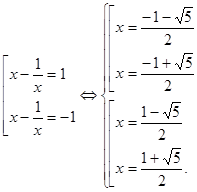

Ответ:

Пример 10.

Решение. Поскольку в левой части стоит сумма двух квадратов, естественно попытаться дополнить её до квадрата суммы или разности. Во втором случае получим