Контрольная работа: Метод замены неизвестного при решении алгебраических уравнений

Итак, надо решить систему

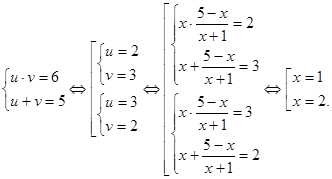
Ответ:

Пример 5. Решить уравнение

Решение. Заметим, что суммы чисел, стоящих во второй и четвёртой, в первой и третьей скобках, равны, т.е. -7+2=-1–4. Перемножив эти пары скобок, приходим к уравнению

Введём замену: получим Решив квадратное уравнение , находим, что или .

Возвращаемся к исходной переменной и решаем совокупность уравнений:

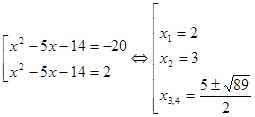
Ответ: .

Пример 6. Решить уравнение

Решение. Заметим, что произведение чисел, стоящих в первой и третьей, во второй и четвёртой скобках, равны, т.е. Перемножим указанные пары скобок и запишем уравнение

Поскольку – не корень, разделим обе части уравнения на Получим:

Введя замену: запишем исходное уравнение в следующем виде:

т.е.

Отсюда . Вернёмся к исходной переменной:

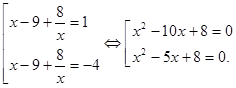
Первое уравнение совокупности имеет корни . Второе уравнение не имеет корней.

Ответ:

Пример 7. Решить уравнение

Решение. Вид уравнения совсем не подсказывает, что его можно свести к однородному. Преобразуем первый множитель, выделив из него выражение, равное второму множителю, т.е.

Подставляя последнее выражение в исходное уравнение, запишем, что