Контрольная работа: Метод замены неизвестного при решении алгебраических уравнений

Возвращаясь к исходной переменной, придём к совокупности:

Второе уравнение совокупности не имеет решений, а первое даёт два решения, которые и выносятся в ответ.

Ответ:

3. Типизация приёмов введения новых неизвестных при решении алгебраических уравнений

В третьей части курсовой работы осуществим типизацию приёмов введения новых неизвестных при решении алгебраических уравнений.

Введение новых переменных может быть как явным, так и неявным. Классифицируем наши уравнения по способам неявной реализации метода замены переменной:

Использование основного свойства дроби .

Использование основного свойства дроби применяется в уравнениях следующего вида:

где постоянные, .

В таких уравнениях сначала проверяют, является ли корнем уравнения, и производят замену .

Выделение квадрата.

Выделение квадрата двучлена чаще всего встречается при решении уравнений, которые можно привести к такому виду, чтобы одна часть уравнения представляла собой сумму квадратов двучлена.

Переход к системе уравнений .

Этот приём целесообразен при решении уравнений вида

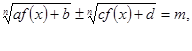
где коэффициенты и равны, противоположны по знаку или отличаются на постоянный множитель.

Раскрытие скобок парами .

Такой методдаёт хороший эффект в уравнениях вида

Где или или

Раскрытие скобок парами и деление обеих частей уравнения .

Раскрытие скобок парами и деление обеих частей уравненияцелесообразно применять в случаях, когда перед нами уравнение вида

где , или или .