Контрольная работа: Метод замены неизвестного при решении алгебраических уравнений

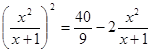
Введём замену: получим

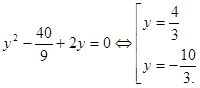
Вернёмся к «старой» переменной:

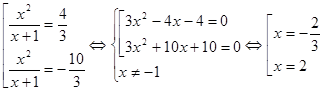
Ответ:

Пример 11.

Решение. Обозначим тогда получим

Обратная замена: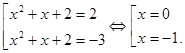

Ответ:

Пример 12.

Решение. Так как не является решением уравнения, то, разделив числитель и знаменатель каждой дроби в левой части на , перепишем его в виде

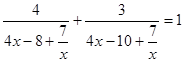
Сделав замену переменных перепишем уравнение в виде

Решения этого уравнения есть

Обратная замена: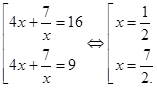

Ответ: .

Пример 13.

Решение. Обозначим через , т.е. сделаем замену переменных или Тогда первоначальное уравнение можно переписать в виде или, применяя формулу в виде

Поскольку корни квадратного уравнения есть , то решения биквадратного уравнения есть

Следовательно, решения исходного уравнения таковы

Ответ:

Пример 14.

Решение . Представляя это уравнение в виде вводим новое неизвестное Уравнение примет вид

Обратная замена: