Контрольная работа: Метод замены неизвестного при решении алгебраических уравнений

Преобразовав один из множителей и выделив из него выражение, равное второму множителю и подставляя полученное выражение в исходное уравнение, удаётся прийти к однородному уравнению второй степени, т.е. к уравнению вида

где - постоянные, отличные от нуля, а , - многочлены.

Тригонометрическая подстановка.

Тригонометрическая подстановка используется в тех случаях, когда область определения исходного уравнения совпадает с областью значения тригонометрической функции или включается в эту область.

4. Комплект типовых задач, сводящихся к применению метода замены при решении уравнений

Исходя из четвёртой задачи курсовой работы, составим комплект типовых задач, сводящихся к применению метода замены при решении уравнений.

Пример 1 .

Решение. ОДЗ уравнения есть все действительные . Сделаем замену неизвестной , где . Тогда исходное уравнение запишется в виде

(1)

, то уравнение (1)

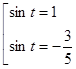
Из решения этих уравнений промежутку принадлежат только . Поэтому

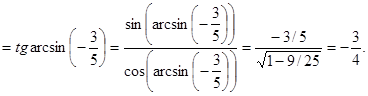
Ответ:

Пример 2 .

Решение. Если сделать замену уравнение упрощается, но остаётся иррациональным. Существенного продвижения можно достичь, если ввести новую переменную:

или посторонний корень

Ответ:

Пример 3 .

Решение. Видим, что к данному уравнению можно применить ранее указанный нами приём – «раскрытие скобок парами». Суммы чисел, стоящих в первой и четвёртой, во второй и третьей скобках, равны, т.е. 1+5=2+4. Перемножив эти пары скобок, приходим к уравнению:

Введём замену: , получим Решив квадратное уравнение находим, что или

Возвращаемся к исходной переменной и решаем совокупность уравнений:

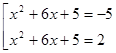
В первом уравнении совокупности корней нет.

Перепишем второе уравнение:

Ответ:

Пример 4 .