Контрольная работа: Производная и ее применение для решения прикладных задач

Решение

Найдем участки возрастания и убывания функции . Производная этой функции равна . Так как дискриминант квадратного трехчлена является отрицательным числом и коэффициент при этого квадратного трехчлена больше нуля, то для каждого действительного х имеем неравенство .

Таким образом, функция является непрерывной и возрастающей на всей числовой прямой; поэтому ее график может пересекать ось ОХ только в одной точке. Учитывая, что , заключаем, что решениями данного неравенства являются все числа х из промежутка .

Пример 2.

Докажите неравенство (при ).

Доказательство.

При х=0 неравенство справедливо.

Рассмотрим функцию и найдем ее производную:

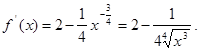Производная обращается в нуль при

При то есть функция монотонно убывает. При то есть функция монотонно возрастает. При функция имеет минимум, равный нулю.

Таким образом, при значит .

Пример 3.

Доказать, что при имеет место неравенство

Решение.

Найдем участки возрастания и убывания функции

Так как то

при

при

при

Функция непрерывна на поэтому она возрастает на отрезке и убывает на промежутке Отсюда заключаем, что точка является точкой локального максимума функции (рис.).

Так как и то неравенство доказано.

3.10 Доказательство тождеств

Пример 1.

Решение

Рассмотрим функцию

.

При х=1 имеем . Пусть ; тогда