Контрольная работа: Производная и ее применение для решения прикладных задач

В данном случае будем считать х=5, а . Изменение функции

3.5 Нахождение величины угла между прямыми и кривыми.

Углом между графиками функций и в точке их пересечения называется угол между касательными к их графикам в этой точке (рис.).

Пример 1.

Найти угол между графиками функций и

в точке их пересечения (с положительной абсциссой).

Решение.

Абсциссы точек пересечения данных графиков удовлетворяют уравнению

И тем самым следующей системе: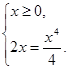

Отсюда находим, что графики функций пересекаются в двух точках, абсциссы которых равны 0 и 2. Найдем тангенсы углов наклона касательных к обоим графикам функций в точке с абсциссой, равной 2. Имеем

Отсюда и Так как , то уравнения касательных к графикам функций и в точке (2;2) соответственно имеют вид

и

т.е.

и

Следовательно величина угла между касательными удовлетворяют уравнению

и тем самым графики функций и в точке с абсциссой х=2 пересекаются под углом, равным

3.6 Разложение на множители и упрощение выражений.

Пример 1.

Разложить на множители выражение

.

Решение:

Считая х переменной величиной, рассмотрим функцию . Имеем .

Так как ,

то отсюда заключаем, что

.