Курсовая работа: Алгоритм Кеннета-Джексона для опису фазових перетворень у бінарних сплавах. Опис дифузії

Різницеві рівняння для дифузії в 1D будуть записані в звичайному вигляді, але з використанням усереднення потоків двох видів. Потік атомів А у напрямку, протилежному потоку атомів B, тому потоки просумовані зі збереженням знака потоку атомів А.

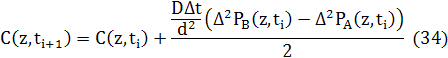
де D=d² Γ/6, d- міжплощинний інтервал, і

Тут D - є дифузія в одиницях довжина² /час, d - міжплощинний інтервал, а Δt - збільшення часу між ітераціями. Хоча структури тут описані одномірною змінною, ця модель є тривимірною, з площинними змінними структури що описані однією змінною. Для того, щоб зробити результати 1D
співрозмірними з 3D результатами ми вирішили включити стрибки у площині в стрибок швидкості, і, отже, стрибок швидкості в будь якому одному напрямку дорівнює 1/6 від загальної швидкості стрибка.

Рівняння такого типу не можуть бути вирішені аналітично, але вони можуть бути легко обчислені чисельно.

5.3 Рівння в кінцевих різницях для дифузії в 2D

Як і для 1Dрізницеве рівняння для дифузії може бути записане в звичайній формі використовуючи усереднення двох потоків.

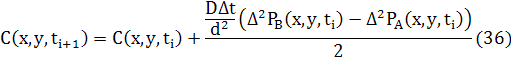
де

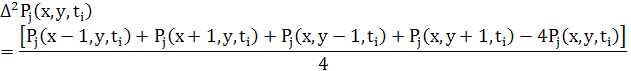
5.4 Різницеві рівняння для дифузії в 3D

Як і для 1D і 2D, різницеве рівняння для дифузії може бути записане в звичайній формі з використання усереднення двох потоків

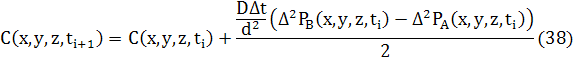
де

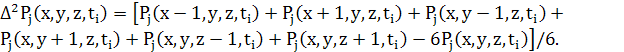(40)

Коли параметр регулярного розчину, Ω = WZ, дорівнює нулю, ці диференціальні рівняння зводяться до стандартних рівнянь дифузії.

5.5 Безрозмірний час

Безрозмірний час, τ, дорівнює

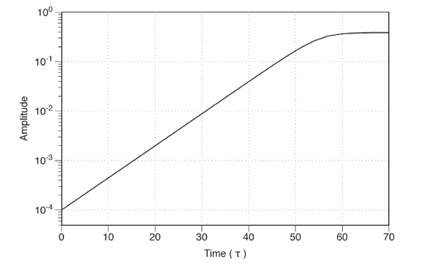
Рис.3.Логарифм зростання амплітуди синусоїдального збурення в часі

Для окремих випадків, множення на d² /D буде