Курсовая работа: Численные методы анализа

Приближенное значение корня х = 0,5629

4. Численные методы вычисления определенных интегралов

4.1 Исходные данные

Интеграл	Шаг	Точность
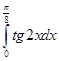		0,001

Вычислим интеграл по формуле Ньютона-Лейбница.

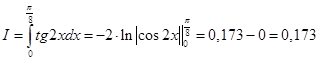
Вычислим значения подынтегральной функции в точках разбиения x_i , где i = 0,1,2..n.

00,4142

0,09850,5345

0,1989 0,6682

0,3033 0,8207

1

Результаты сведены в таблицу:

i	0	1	2	3	4	5	6	7	8
x	0
f( x )	0	0,0985	0,1989	0,3033	0,4142	0,5345	0,6682	0,8207	1

4.2 Вычислим интеграл методом левых прямоугольников

I_лп = h·[f(x₀ ) + f(x₁ ) + f(x₂ ) + … + f(x_{n -1} )] = ·[0+0,0985+0,1989+0,3033+0,4142+0,5345+0,6682+0,8207] = 0,1491

Ошибка вычисления:

О = |0,173–0,1491| = 0,0239 = 0,001 – нет.

4.3 Вычислим интеграл методом правых прямоугольников

I_пп = h·[f(x₁ ) + f(x₂ ) + f(x₃ ) + … + f(x_n )] = ·[0,0985+0,1989+0,3033+0,4142+0,5345+0,6682+0,8207+1] = 0,1982

Ошибка вычисления:

О = |0,173–0,1982| = 0,0252 = 0,001 – нет.

4.4 Вычислим интеграл методом центральных прямоугольников

Вычислим значения подынтегральной функции в центре каждого выделенного интервала:

0,04910,4730

0,14830,5994

0,25050,7416

0,35780,9063

Результаты сведены в таблицу:

i	1	2	3	4	5	6	7	8
x
f с ( x )	0,0491	0,1483	0,2505	0,3578	0,4730	0,5994	0,7416	0,9063