Курсовая работа: Діафантові рівняння

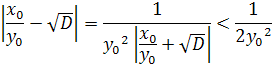
Тобто – однин із підхідних дробів до . Оскільки , щозадовольняють рівняння (6) є взаємно простими числами, то із рівності

випливає: = .

Розклад в ланцюговий дріб в загальному виглядає так:

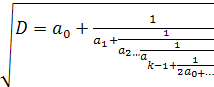(7)

Виявляється, що розв’язками рівняння (6) можуть бути чисельники і знаменники тільки тих підхідних дробів до у яких індекс 𝑠 має вид .

Теорема 7.

Якщо ( ) – розв'язок діофантового рівняння (6), то , де - підхідний дріб до .

Доведення. В попередній теоремі було доведено, що якщо пара цілих додатних чисел є розв’язком рівняння (6), то = , де - підхідний дріб до . Число є коренем квадратного рівняння з цілими коефіцієнтами

. (8)

Повний частковий розклад в ланцюговий дріб є коренем деякого квадратного рівняння

з тим же дискримінантом, як у рівнянні (8) (при ) маємо:

;

- парне число, яке позначимо - 2. Розв’язуючи квадратне рівняння для ,отримаємо , тобто розклад в ланцюговий дріб повинен мати той же період, як і в розкладі (7) числа і відрізняється від нього тільки на перший член розладу. Це може бути тільки при , , . Тепер залишається тільки вияснити, які саме з чисел є розв’язками рівняння (6).

Теорема.

Нехай 𝐷 – ціле додатне, вільне від квадратів число, 𝑘 – довжина періоду розкладу в ланцюговий дріб. Ми отримаємо всі розв’язки рівняння (6) в цілих додатних числах 𝑥 та 𝑦, якщо візьмемо:

де 𝑛 – довільне натуральне число, таке, що 𝑘𝑛 парне.

Доведення.

В попередній теоремі було встановлено, що всі цілі додатні розв’язки рівняння (6) знаходяться серед пар вигляду . Залишається тільки вияснити, при яких 𝑛 числа задовольняють рівняння (6).

врозкладі в ланцюговий дріб має вигляд:

,

тобто (8).

Так, що підставляючи значення із формули (8), отримаємо:

(9)

Оскільки - ірраціональне, із рівності (9) випливає: