Курсовая работа: Интегралы, зависящие от параметра

Если использовать определение предела функции по Гейне, то можно

сформулировать

Предложение 2.1 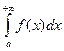сходится тогда и только тогда, когда

для любой последовательности →+∞, последовательность интегралов сходится

Определение 2. 2. Назовем интеграл абсолютно сходящимся, если сходится интеграл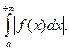

Теорема 2.2. Если сходится абсолютно, то он сходится.

Доказательство. Так как интеграл сходится абсолютно, то по критерию Коши выполняется условие

Но тогда и

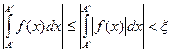
При любых ■

Определение 2.3. Если сходится, но не сходится абсолют-

но, то будем называть его условно сходящимся.

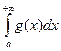Теорема 2.3 (Вейерштрасс). Пусть функции f, g: [а; +∞) →R, интегрируемы по Риману на [а; А] при любом А > а, для всех и сходится. Тогда 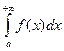тоже сходится и притом абсолютно.

Доказательство. Так как 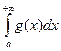сходится, то по критерию Коши 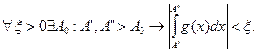Но тогда при А’, А” > имеем:

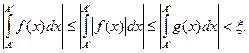
Из полученной оценки, в силу критерия Коми, вытекает и сходимость и абсолютная сходимость интеграла от f(x) •

Замечание 2.1 . Неравенство в формулировке теоремы может выполняться лишь для , где b>a. Это вытекает из того, что всегда можно представить

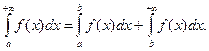
Первый интеграл в этом представлении не особенный, а ко второму можно применить доказанную теорему.

Пример 2.2 Рассмотрим интегралы

Решение. Так как а сходится, если р> 1 (пример2.1) то и сходится, и притом абсолютно, при р > 1. Второй интеграл рассматривается

аналогично. ■

Теорема 2.4 (Дирихле) Пусть функции f, g: и интегрируемы по Риману

на [а; А] при любом А > а. Тогда 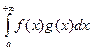сходится, если выполнены следующие

два условия:

1) 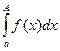ограничен на [а; +∞);

2) функция g(x) монотонно стремится к нулю при

Доказательство. По первому условию существует постоянная М такая,

что . По второму условию такое, что при А > будет выполняться неравенство . По второму же условию функцию g(x) можно считать неотрицательной. Возьмём и применим к интегралу вторую теорему о среднем значении (формулу Боннэ), согласно которой найдётся такое, что

Но тогда, поскольку