Курсовая работа: Интегралы, зависящие от параметра

Возьмём и применим к интегралу вторую теорему о среднем значении (только на этот раз в общем виде, поскольку неизвестен знак g(х, у)), согласно которой найдётся А = А(у), А [А’, А”], такое, что

(2.18)

Оценим (2.18) с помощью (2.16) и (2.17).

для любого у из множества Y.

Используя критерий Коши, получаем требуемое утверждение. ■

Теорема 2.15 (Абель) Пусть функции f, g : [а; +∞) х Y→R и

интегрируемы по Риману на [а; А] при любых А > а и у . Тогда

сходимся равномерно на Y, если выполнены следующие два условия:

1) сходимся равномерно на множестве Y;

2)функция g(х, у) монотонна по х при каждом у и равномерно

по у ограничена, то есть, существует постоянная М такая, что

для всех х [а; +∞) и у .

Пример 2.12 Рассмотрим 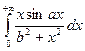, где b> 0 постоянная, а параметр а удовлетворяет условию

Решение. Положим f(x,a)= sinax, g(x,a) Тогда

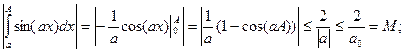
при х → +∞, и это условие (ввиду независимости функции g от а) вы-

полнено равномерно по а.

Так как оба условия признака Дирихле выполнены, то рассматриваемый интеграл сходится равномерно в указанной области. ■

Пример 2.13 Рассмотрим 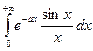(a≥0)

Решение. Положим f(x, а) = , g(х, а) = . Так как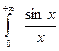

сходится равномерно по а (ввиду его отсутствия) по признаку Дирихле,

а функция , очевидно, монотонна по х и при х ≥ 0, у ≥0 ограничена,

то рассматриваемый интеграл сходится равномерно в указанной области

по признаку Абеля.■

2.4 Свойства несобственных интегралов, зависящих

от параметра

Изучим свойства несобственных интегралов первого рода, зависящих

от параметра, ограничившись простейшим случаем: множество Y есть

отрезок [с; d] вещественной оси. Введём обозначение

и докажем предварительно следующую лемму.

Лемма 2.1 Если интеграл (2.13) сходится равномерно на множестве Y

то последовательность функций

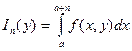,() (2.19)