Курсовая работа: Интегралы, зависящие от параметра

Выполнила: студентка ФМФ 33 гр.

Сыпко Галина Александровна.

Научный руководитель: ассистент

Анохина Е.Ю.

Таганрог. 2009 г.

Содержание

1 Введение…………………………………………………………………….3

2 Интегралы, зависящие от параметра…………………………...................4

2.1 Несобственные интегралы…………………………………………….4

2.2 Собственные интегралы, зависящие от параметра…………………11

2.3 Несобственные интегралы, зависящие от параметра………………17

2.4 Свойства несобственных интегралов, зависящих от параметра…..21

2.5 Вычисление интегралов, зависящих от параметра………………….25

3 Список литературы…………………………………………………………27

1 Введение.

Математический анализ - общеобразовательная математическая дисциплина, объектом изучения которой является большая часть математики, связанная с понятиями функции, производной и интеграла. Цель дисциплины «Математический анализ»- ознакомление с фундаментальными методами исследования переменных величин посредством анализа бесконечно малых, основу которого составляет теория дифференциального и интегрального исчисления.

Объектами изучения в данной дисциплине являются прежде всего функции. С их помощью могут быть сформулированы как законы природы, так и разнообразные процессы, происходящие в технике. Отсюда объективная важность математического анализа как изучения функций.

2 Интегралы, зависящие от параметра .

2.1Несобственные интегралы.

Несобственные интегралы первого рода.

Пусть f :[a, +R и интегрируема по Риману на любом отрезке [a, A] (A(а,Формальное выражение

назовем несобственным интегралом первого рода.

Определени2.1 Несобственный интеграл первого рода назовем сходящимся, если существует

В этом случае будем говорить, что число I является значением интеграла и писать

Если же указанный предел равен бесконечности или вовсе не существует, то будем говорить, что интеграл расходится.

При аналогичных предложениях определим несобственные интегралы

и

Пример.2.1 . Исследовать на сходимость интеграл

∆Пусть тогда

Если , то существует конечный то есть интеграл J сходится, причем Если то и поэтому интеграл J расходится. При интеграл также расходится, так как при

Таким образом, интеграл J сходится при и расходится при ▲

Теорема 2.1 (критерий Коши) Для сходимости несобственного интеграла

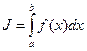
Необходимо и достаточно, чтобы выполнялось условие Коши

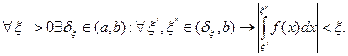(1)

○ Обозначим

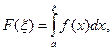
(2)

Тогда сходимость интеграла J означает существование конечного предела функции при а этот предел, согласно критерию Коши для функций, существует в том и только том случае, когда функция F удовлетворяет условию

(3)

Из формулы (2) в силу свойств интеграла следует, что

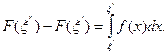
--> ЧИТАТЬ ПОЛНОСТЬЮ <--