Курсовая работа: Интегралы, зависящие от параметра

Замечание 2.3 Условия теорем 2.7 — 2.11 являются достаточными.

декларируемые в теоремах свойства могут выполняться и при нарушении условий этих теорем. Но быть уверенным в их выполнении при нарушении условий теорем нельзя.

Рассмотрим соответствующие примеры.

Пример 2.8 Рассмотрим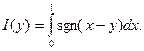

Решение. Подынтегральная функция на прямой у = х терпит разрыв.

Однако, вычислив интеграл, убедимся, что он представляет непрерывную функцию от у на всей вещественной прямой.

1. Пусть у≤ 0. ;

2.Пусть о< у <1. I(у)=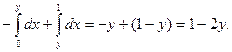

3.Пусть у ≥ 1.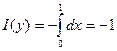

Нетрудно убедиться, что функция ‚ I(у) имеет одинаковые пределы

слева и справа в точках у = 0 и у = 1, поэтому непрерывна. ■

Пример 2.9 Рассмотрим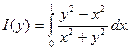

Решение . Подынтегральная функция терпит разрыв в точке (0; 0), однако, вычислив интеграл, убедимся, что он представляет интегрируемую

на отрезке [0; 1] функцию.

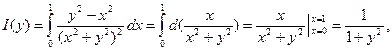
поэтому

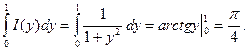
Однако попытка проинтегрировать по параметру под знаком интеграла приведёт к иному результату.

■

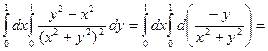
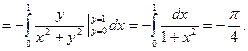Пример 2.10 Рассмотрим

Решение. Легко видеть, что интеграл удовлетворяет условиям теоремы 2.11 на любом отрезке [с; d]. Найдём производную I’(y), используя формулу 2.8.

2 .3 Несобственные интегралы, зависящие от параметра

Пусть Y — произвольное множество, f: [а; +∞) х Y → R. Предположим, что для каждого у сходится . Тогда на множестве

Y определена функция

( 2 .1 3 )

которую будем называть несобственным интегралом первого рода, зависящим от параметра.

Равномерна я сходимость

Понятие равномерной сходимости для несобственных интегралов, зависящих от параметра, столь же важно, как и для функциональных рядов.

Определение 2.8 Будем говорить, что интеграл (2.13) сходится равномерно на множестве Y , если его остаток равномерно стремится к нулю на этом множестве, то есть, если такое, что выполняется неравенство

(2.14)