Курсовая работа: Интегралы, зависящие от параметра

Первый из интегралов — интеграл с постоянными пределами вида

2.1, его непрерывность доказана в теореме 2.7. Поэтому

Займемся вторым интегралом. Функция f(x, у) непрерывна на П, следовательно, ограничена. Поэтому существует постоянная М такая, что

П. Но тогда

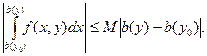
А так как функция b(у) непрерывна на [с; d], то при

, поэтому

Совершенно аналогично доказывается, что и

Таким образом,

что и требовалось доказать. ■

Теорема 2.11 Пусть функция f непрерывна на прямоугольнике П и

имеет на нём непрерывную частную производную , а функции а(у) и

b(у) дифференцируемы на отрезке [с; d]. Тогда функция I(у), определяемая равенством (2.6), дифференцируема на отрезке [с; d] и её производная может быть вычислена по формуле

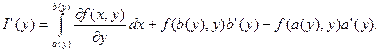(2.8)

Доказательство. Поскольку дифференцируемость на промежутке есть

дифференцируемость в каждой точке промежутка, то возьмём на отрезке [с; d] и покажем, что I(у) дифференцируема в точке , и что представляется в виде правой части формулы (2.8). Для этого воспользуемся представлением I(у) в виде (2.7) и покажем, что каждое слагаемое

правой части (2.7) дифференцируемо и вычислим его производную.

Первый из интегралов в правой части (2.7) имеет постоянные пределы

интегрирования. Его дифференцируемость установлена в теореме 2.9.

Поэтому

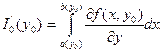(2.9)

Теперь докажем дифференцируемость и вычислим производную второго слагаемого в правой части (2.7). (Отметим, что .)

По определению производной

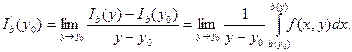
Так как подынтегральная функция непрерывна (по х), то по свойству

определённого интеграла найдётся с = с(у), , такое, что

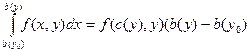. Но тогда

так как первый предел существует по теореме о трёх функциях и в силу непрерывности функции f на прямоугольнике П, а второй — в силу

дифференцируемости функции b(у). Итак,

. (2.10)

Совершенно аналогично доказывается, что третье слагаемое в (2.7)

дифференцируемо и что

. (2.11)

Итак, все три слагаемых в правой части равенства (2.7) дифференцируемы в точке , значит, и функция I(у) дифференцируема в точке и

. (2.12)

Подставив сюда значения производных (формулы (2.9), (2.10), (2.11)),