Курсовая работа: Интегралы, зависящие от параметра

Кантора функция f равномерно непрерывна на П, следовательно, по выбранному >0 можно указать такое > 0, что если

то будет выполняться неравенство

Положим х' = х"= х, у' = у, у" =. Тогда

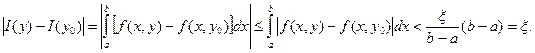
Полученная оценка доказывает не только непрерывность, но и равномерную (поскольку δ не зависит от ) непрерывность функции I(у) на

отрезке [а; b].■

Теорема 2.8 Пусть функция f непрерывна на прямоугольнике П. Тогда

функция I(у) интегрируема на отрезке [с; d] и справедливо равенство

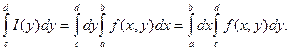(2.2)

Доказательство . Интегрируемость I(у) вытекает из предыдущей теоремы и теоремы об интегрируемости непрерывных функций. Равенство

же 2.2 следует из теоремы о сведении кратного интеграла к повтор-

ному. для непрерывной на прямоугольнике П функции существует

, который может быть сведен к повторному в любом порядке. ■

Теорема 2.9 Если функция f непрерывна и имеет непрерывную частную производную на прямоугольнике П, то функция I(у) дифференцируема на отрезке [с; d] и справедливо равенство

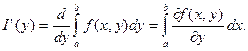(2.3)

Доказательство. Так как непрерывна на П, то, используя предыдущую теорему, для любого у [с; d] можем написать равенство

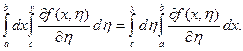(2.4)

Упростим левую часть равенства 2.4 с помощью формулы Ньютона-

Лейбница.

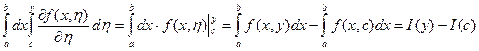
Обозначим через J(η) внутренний интеграл в правой части равенства

(2.4). Тогда равенство (2.4) примет вид:

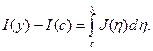(2.5)

По теореме 2.7 J(η) — непрерывная на [с; d] функция. Но тогда по

теореме о производной интеграла с переменным верхним пределом правая часть равенства (3.5) (следовательно, и левая) дифференцируема на

отрезке [с; d]. По той же теореме из равенства (3.5) получаем:

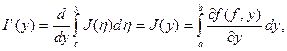
что и требовалось. ■

Рассмотрим теперь более общий случай, когда не только подынтегральная функция, но и пределы интегрирования зависят от параметра. Итак, пусть функция f(x, у) определена на прямоугольнике П =[а; Ь] х [с; d], интегрируема по х на отрезке [а; b] для каждого у [с; d],

функции а (у) и b(у) заданы на отрезке [с; d] и [с; d] выполняется

а ≤ а(у) ≤ b(у) ≤ b. Рассмотрим интеграл

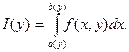(2.6)

Теорема 2.10 Пусть функция f(x, у) непрерывна на П, а функции а(у),

b(у) непрерывны на [с; d]. Тогда функция I(у), определённая равенством

(2.6), непрерывна на [с; d].

Доказательство. Пусть y [с; d]. Покажем, что Для этого разобьём интеграл на три слагаемых, используя свойство аддитивности интеграла.

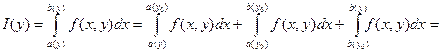
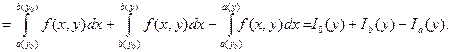(2.7)

Здесь интегралы обозначены в порядке следования. Рассмотрим каждый