Курсовая работа: Интегралы, зависящие от параметра

для любых А’, А” > . По критерию Коши интеграл сходится. ■

Теорема 2.5 (Абель) Пусть функции f, g : [а; +∞)→R и интегрируемы по Риману на [а; А] при любом А > а. Тогда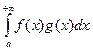 сходится, если выполнены следующие два условия:

1) сходится;

2) функция g(x) монотонна и ограничена на [а; +∞).

Доказательство. В силу второго условия существует.

Тогда

Первый из интегралов справа сходится по признаку Дирихле, поскольку

монотонно стремится к нулю при х→+∞, а второй сходится в силу условия 1 доказываемой теоремы. ■

Замечание 2.2 При доказательстве теоремы Абеля было использовано очевидное свойство

несобственных интегралов: если сходятся интегралы и , то сходится и, при этом

=+

Пример 2.3 Вернемся к рассмотренным выше примерам

Решение. По признаку Дирихле эти интегралы сходятся при р > 0, поскольку при этом условии дробь ↓ 0, а интегралы очевидно, ограничены. ■

Пример 2.4 Рассмотрим

Решение. Этот интеграл сходится по признаку Абеля. Действительно,

сходимость интеграла установлена в предыдущем примере, а

функция arctg х монотонна и ограничена. ■

Несобственные интегралы второго рода

Пусть функция f : (а; b] →R, неограниченна в окрестности точки а, но интегрируема по Риману на [а + δ, b] при любом 0<δ<b-a.

Формальное выражение

назовём несобственным интегралом второго рода.

Определение 2.4 Несобственный интеграл второго рода назовём сходящимся, если существует

В этом случае будем говорить, что число I являемся значением интеграла и писать

Если же указанный предел равен бесконечности или вовсе не существует, то будем говорить, что интеграл расходится.

Аналогично определяется

если функция f определена на [а; b), интегрируема на [а; b-ξ] при любом 0<δ<b-a и неограниченна в окрестности точки b.

Если же функция f определена на [а; b]\{c}, а < с < b, неограниченна в окрестности точки с, но интегрируема на отрезках [а; с-δ] и [с-δ; b] при любом допустимом положительном δ, то определим