Курсовая работа: Колебания

где введена комплексная величина

(2,9)

Уравнение (2,8) уже не второго, а первого порядка. Без правой части его решением было бы

с постоянной А . Следуя общему правилу, ищем решение неоднородного уравнения в виде

и для функции A ( t ) получаем уравнение

Интегрируя его, получим решение уравнения (2,8) в виде

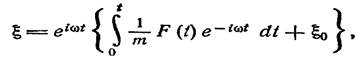(2, 10)

где постоянная интегрирования ε0 представляет собой значение ε в момент времени t = 0. Это и есть искомое общее решение; функция x ( t ) дается мнимой частью выражения (2,10).

Энергия системы, совершающей вынужденные колебания, разумеется, не сохраняется; система приобретает энергию за счет источника внешней силы. Определим полную энергию, передаваемую системе за все время действия силы (от - ∞ до + ∞), предполагая начальную энергию равной нулю. Согласно формуле (2,10) (с нижним пределом интегрирования - ∞ вместо нуля и с

ξ (-∞) = 0) имеем при t → ∞:

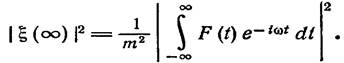
С другой стороны, энергия системы как таковой дается выражением

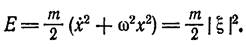(2,11)

Подставив сюда | ξ (∞) |² , получим искомую передачу энергии

в виде

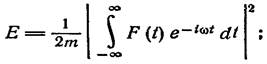(2,12)

она определяется квадратом модуля компоненты Фурье силы F ( t ) с частотой, равной собственной частоте системы.

В частности, если внешняя сила действует лишь в течение короткого промежутка времени (малого по сравнению с 1/ω ), то можно положить .

Тогда

Этот результат заранее очевиден: он выражает собой тот факт, что кратковременная сила сообщает системе импульс ∫F dt , не успев за это время произвести заметного смещения.

Колебания систем со многими степенями свободы

Теория свободных колебаний систем с несколькими (s) степенями свободы строится аналогично тому, как было рассмотрено в одномерных колебаниях.

Пусть потенциальная энергия системы U как функция обобщенных координат qi ( i = 1, 2, .,., s ) имеет минимум при qi = qi 0 . Вводя малые смещения

xi = qi – qi 0 (3,1)