Курсовая работа: Колебания
Каждой кратной (или, как говорят, вырожденной ) частоте отвечает столько различных нормальных координат, какова степень кратности, но выбор этих нормальных координат не однозначен. Поскольку в кинетическую и потенциальную энергии нормальные координаты (с одинаковым ωа ) входят в виде одинаково преобразующихся сумм 
можно подвергнуть любому линейному преобразованию, оставляющему инвариантной сумму квадратов.
Весьма просто нахождение нормальных координат для трехмерных колебаний одной материальной точки, находящейся в постоянном внешнем поле. Помещая начало декартовой системы координат в точку минимума потенциальной энергии U ( x , y , z ), мы получим последнюю в виде квадратичной формы переменных х, у, z , а кинетическая энергия
(т — масса частиц) не зависит от выбора направления координатных осей.
Поэтому соответствующим поворотом осей надо только привести к диагональному виду потенциальную энергию. Тогда
(3,14)
и колебания вдоль осей х, у, z являются главными с частотами
В частном случае центрально-симметричного поля (k 1= k 2= k 3= k , U = kr ²/2 ) эти три частоты совпадают.
Использование нормальных координат дает возможность привести задачу о вынужденных колебаниях системы с несколькими степенями свободы к задачам об одномерных вынужденных колебаниях. Функция Лагранжа системы с учетом действующих на нее переменных внешних сил имеет вид
(3,15)
где L0 — лагранжева функция свободных колебаний. Вводя вместо координат хk нормальные координаты, получим:
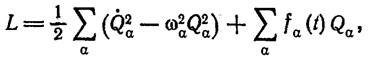(3.16)
где введено обозначение
Соответственно уравнения движения
будут содержать лишь по одной неизвестной функции Qa (t).
Затухающие колебания
До сих пор мы всегда подразумевали, что движение тел происходит в пустоте или что влиянием среды на движение можно пренебречь. В действительности при движении тела в среде последняя оказывает сопротивление, стремящееся замедлить движение. Энергия движущегося тела при этом в конце концов переходит в тепло или, как говорят, диссипируется.
Процесс движения в этих условиях уже не является чисто механическим процессом, а его рассмотрение требует учета движения самой среды и внутреннего теплового состояния как среды, так и тела. В частности, уже нельзя утверждать в общем случае, что ускорение движущегося тела является функцией лишь от его координат и скорости в данный момент времени, т. е. не существует уравнений движения в том смысле, какой они имеют в механике. Таким образом, задача о движении тела в среде уже не является задачей механики.
Существует, однако, определенная категория явлений, когда движение в среде может быть приближенно описано с помощью механических уравнений движения путем введения в них некоторых дополнительных членов. Сюда относятся колебания с частотами, малыми по сравнению с частотами, характерными для внутренних диссипативных процессов в среде. При выполнении этого условия можно считать, что на тело действует сила трения, зависящая (для заданной однородной среды) только от его скорости.
Если к тому же эта скорость достаточно мала, то можно разложить силу трения по ее степеням. Нулевой член разложения равен нулю, поскольку на неподвижное тело не действует никакой силы трения, и первый неисчезающий член пропорционален скорости. Таким образом, обобщенную силу трения fтр, действующую на систему, совершающую одномерные малые колебания с обобщенной координатой х, можно написать в виде
где а — положительный коэффициент, а знак минус показывает, что сила действует в сторону, противоположную скорости. Добавляя эту силу в правую сторону уравнения движения, получим :
(4.1)
Разделим его на m и введем обозначения
(4.2)