Курсовая работа: Колебания

Вещественность и положительность корней уравнения (3,8) заранее очевидны уже из физических соображений. Действительно, наличие у ω мнимой части означало бы наличие во временной зависимости координат х k (3,6) (а с ними и скоростей x_k ) экспоненциально убывающего или экспоненциально возрастающего множителя. Но наличие такого множителя в данном случае недопустимо, так как оно привело бы к изменению со временем полной энергии E=U+T системы в противоречии с законом ее сохранения.

В том же самом можно убедиться и чисто математическим путем. Умножив уравнение (3,7) на и просуммировав затем по i , получим:

откуда

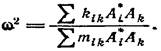
Квадратичные формы в числителе и знаменателе этого выражения вещественны в силу вещественности и симметричности коэффициентов kik и mik , действительно,

Они также существенно положительны, а потому положительно и ω² .

После того как частоты ω_а найдены, подставляя каждое из них в уравнения (3,7), можно найти соответствующие значения коэффициентов А k . Если все корни ω_а характеристического уравнения различны, то, как известно, коэффициенты Ak пропорциональны минорам определителя (3,8),в котором ω заменена соответствующим значением ω_а , обозначим эти миноры через ∆ka . Частное решение системы дифференциальных уравнений (3,5) имеет, следовательно, вид

где С_а — произвольная (комплексная) постоянная.

Общее же решение дается суммой всех s частных решений. Переходя к вещественной части, напишем его в виде

(3,9)

Где мы ввели обозначение

(3,10)

Таким образом, изменение каждой из координат системы со временем представляет собой наложение s простых периодических колебаний

Θ1, Θ2, … , Θs с произвольными амплитудами и фазами, но имеющих вполне определенные частоты.

Естественно возникает вопрос, нельзя ли выбрать обобщенные координаты таким образом, чтобы каждая из них совершала только одно простое колебание? Самая форма общего интеграла (3,9) указывает путь к решению этой задачи.

В самом деле, рассматривая s соотношений (3,9) как систему уравнений с s неизвестными величинами Θ_а , мы можем, разрешив эту систему, выразить величины Θ1, Θ2, …, Θs через координаты x1, x2, ..., x_s . Следовательно, величины Θ_а можно рассматривать как новые обобщенные координаты. Эти координаты называют нормальными (или главными), а совершаемые ими простые периодические колебания — нормальными колебаниями системы.

Нормальные координаты Θ_а удовлетворяют, как это явствует из их определения, уравнениям

(3,11)

Это значит, что в нормальных координатах уравнения движения распадаются на s независимых друг от друга уравнений. Ускорение каждой нормальной координаты зависит только от значения этой же координаты, и для полного определения ее временной зависимости надо знать начальные значения только ее же самой и соответствующей ей скорости. Другими словами, нормальные колебания системы полностью независимы.

Из сказанного очевидно, что функция Лагранжа, выраженная через нормальные координаты, распадается на сумму выражений, каждое из которых соответствует одномерному колебанию с одной из частот ω_а , т. е. имеет вид

(3,12)

где т_а — положительные постоянные. С математической точки зрения это означает, что преобразованием (3,9) обе квадратичные формы — кинетическая энергия (3,3) и потенциальная (3,2) — одновременно приводятся к диагональному виду.

Обычно нормальные координаты выбирают таким образом, чтобы коэффициенты при квадратах скоростей в функции Лагранжа были равны 1/2. Для этого достаточно определить нормальные координаты (обозначим их теперь Q_a ) равенствами

(3.13)

Тогда