Курсовая работа: Некоторые интерполяционные свойства конечномерных сетевых пространств и пространств Лоренца

Аннотация

В данной курсовой работе исследованы свойства некоторых семейств конечномерных пространств и доказаны интерполяционные теоремы для этих классов пространств.

Содержание

Введение

1. Основные понятия и некоторые классические теоремы теории интерполяции

2. Общие свойства интерполяционных пространств

3. О норме и спектральном радиусе неотрицательныхматриц

4. Некоторые интерполяционные свойства семейств конечномерных пространств

Заключение

Список использованной литературы

Введение

Теория интерполяции функциональных пространств как самостоятельная ветвь функционального анализа сформировалась за последние 40-45 лет. Она играет все возрастающую роль в анализе и его приложениях. Центральной темой теории является проблема интерполяции линейных операторов. Эта проблема тесно связана с задачей построения совокупности "промежуточных" пространств – арены, на которой действуют "промежуточные" операторы. Основополагающий вклад в теорию был сделан Эл.-Л. Лионсом, А.П. Кальдероном и С.Г. Крейном. При этом не следует, конечно, забывать, что исследованием названных авторов предшествовали (и стимулировали их) классические теоремы Рисса и Марцинкевича об интерполяции линейных операторов в пространствах l_p .

Теория интерполяция также применяется в других областях анализа (например, в теории уравнений с частными производными, численном анализе, теории аппроксимации). Рассматривают два существенно различных интерполяционных метода: метод вещественной интерполяции и метод комплексной интерполяции. Модельными примерами для этих методов служат доказательства теоремы Марцинкевича и теоремы Рисса-Торина соответственно. Один из самых ранних примеров интерполяции линейных операторов был предложен Шуром. Шур сформулировал свой результат для билинейных форм, или вернее для матриц, соответствующих этим формам. В 1926 году М. Рисс доказал первую версию теоремы Рисса-Торина с ограничением p≤q, которое как он показал, существенно в случае, когда в качестве скаляров берутся вещественные числа. Основным рабочим инструментом Рисса было неравенство Гельдера. Но в 1938 году Торин привел совершенно новое доказательство и смог устранить ограничение p≤q. В то время как Рисс пользовался вещественными скалярами и неравенством Гельдера, Торин использовал комплексные скаляры и принцип максимума.

1. Основные понятия и некоторые классические теоремы теории интерполяции

Пусть (u,μ) – пространство с мерой μ, которую будем всегда предполагать положительной. Две рассматриваемые функции будем считать равными, если они отличаются друг от друга лишь на множестве нулевой μ-меры. При этом обозначим через l_p (u,dμ) или просто (l_p (dμ), l_p (u) или l_p ) лебегово пространство всех скалярнозначных μ-измерных функций f и u, для которых величина

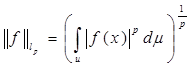
конечна, здесь 1≤p<∞.

В случае, когда p=∞, пространство l_p состоит из всех μ-измеримых ограниченных функций. В этом случае

Пусть T- линейное отображение пространства l_p =l_p (u,dμ) в пространство l_q =l_q (v,dν). Это означает, что T(αf+βg)=αT(f)+βT(g).

Если к тому же T- ограниченное отображение, то есть если величина конечна, то пишут T: lp®lq.

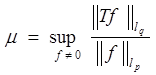
Число μ называется нормой отображения T. Справедливы следующие известные теоремы:

Теорема 1.1 (интерполяционная теорема Рисса-Торина)

Предположим, что и что T: с нормой μ₀ и T : с нормой μ₁ .

Тогда T: → с нормой μ, удовлетворяющей неравенству (*), при условии, что 0<θ<1 и ; .

Неравенство (*) означает, что μ как функция от θ логарифмически выпукла, то есть lnμ – выпуклая функция.

Доказательство теоремы приведено в [1].

Для скалярнозначной μ-измерной функции f, принимающей почти всюду конечные значения, введем функцию распределения m(σ,f) по формуле

--> ЧИТАТЬ ПОЛНОСТЬЮ <--