Курсовая работа: Решение обратных задач динамики
где коэффициенты 
, неизвестны и их необходимо определить.
Следовательно входной сигнал будет зависеть от времени 
и от множества параметров 
Тогда дифференциальное уравнение (2.2) можно записать в следующей виде
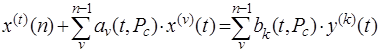(2.5)
Интегрируя уравнение 
раз с учетом начальных условий, получим
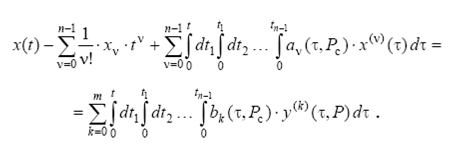(2.6)
Воспользовавшись справедливым для любой непрерывной функции тождеством
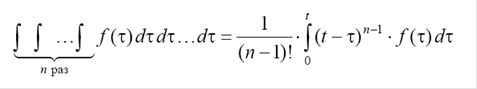
равенство (2.6) можно переписать в виде
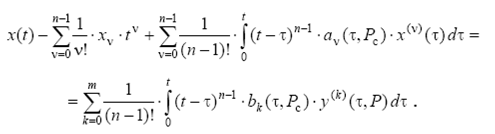(2.7)
Интегрируя полученное равенство (2.7) по частям и применяя формулы
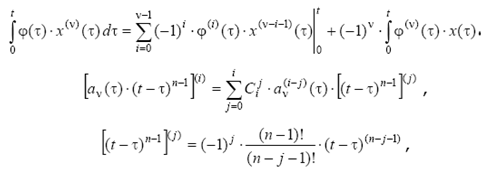
получим
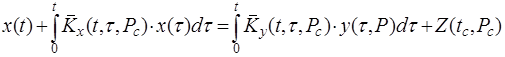(2.8)
где
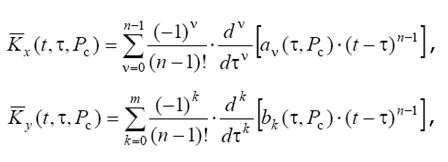
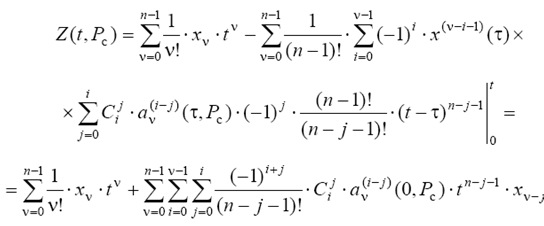
Уравнение (2.8) представляет собой уравнение Вольтера 2-го рода. Преобразуем его к интегральному уравнению Фредгольма 2-го рода на интервале исследования 
:
(2.9)
где
Таким образом, получены две эквивалентные формы описания системы: дифференциальное уравнение (2.2) с начальными условиями (2.3) и интегральное уравнение (2.9). Функция 
в выражении (2.9) представляет собой полином, коэффициенты которого зависят от начальных условий (2.3) и от множества 
искомых параметров настройки системы автоматического управления (регулирования). Перепишем , изменив порядок суммирования
Введем следующие обозначения:
Тогда полином можно записать следующим образом
где 
- вектор-столбец начальных условий; 
- вектор-столбец полиномов 
.
Рассмотрим левую часть уравнения (2.9). Представим функции, входящие в нее, в виде разложений в ряд по ортонормированному базису 
.
Имеем