Курсовая работа: Решение обратных задач динамики

. (2.19)

Здесь спектральная характеристика эталонного сигнала или задана или, в случае задании эталонного сигнала , определяется из выражения

, .

Таким образом, задача определения входного сигнала (точнее множества ) и множества неизвестных параметров настройки системы управления (2.2), (2.3) сводиться к задаче безусловной минимизации функционала (2.18) по элементам множеств и , т.е.

.

На рисунке 2.1 представлена структурная схема алгоритма решения поставленной задачи.

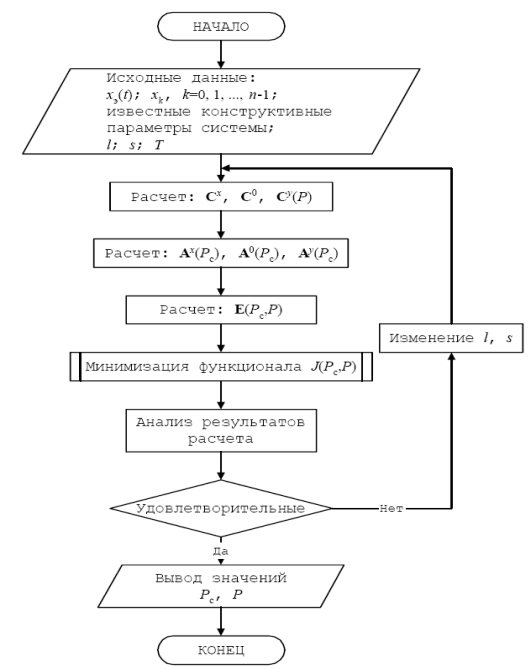
Рис 2.1 Структурная схема алгоритма решения обратной задачи динамики спектральным методом

4. Практическая часть

Рассмотрим отдельный блок системы самонаведения, структурная схема которого представлена на рисунке 1.

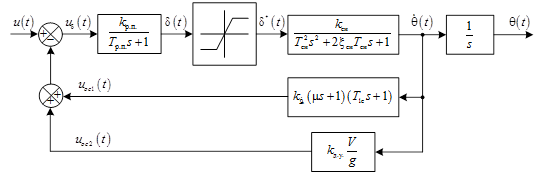
Рис. 1. Структурная схема системы

Задан эталонный закон изменения угла , график которого представлен на рисунке 2.

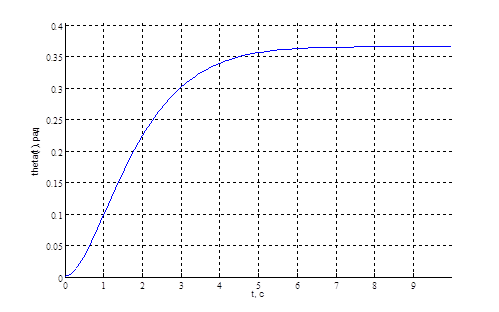
Рис. 2. График эталонного закона изменения угла

Задача формулируется следующим образом. Необходимо найти управление такое, которое обеспечит на выходе сигнал , максимально близкий к заданному эталонному закону.

5. Практическая часть

Данная задача относится к разряду неккоректных и мы будем решать её с применением оптимизационных методов.

Для решения данной задачи воспользуемся методом матричных операторов. В этом случае структурную схему можно представить в следующем виде (рис. 3).

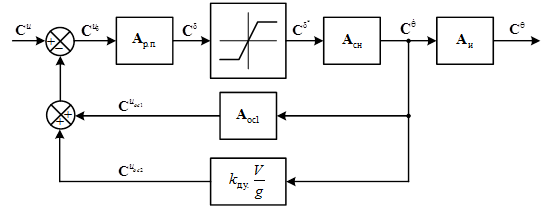
Рис. 3. Структурная схема системы в операторной форме

В качестве ортонормированной системы использовалась система функций Уолша с удержанием элементов. В этом случае матричные операторы основных элементов системы будут следующими (представлены подматрицы размерностью ):

;

;

;

.

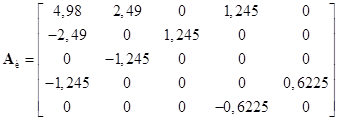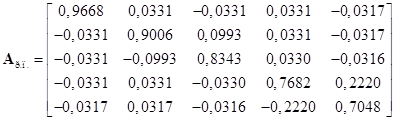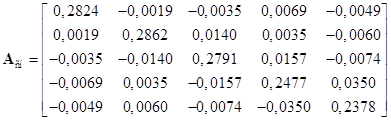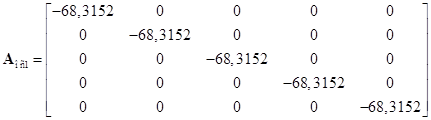Спектральная характеристика сигнала следующая (представлены первые пять элементов):

.

Решение поставленной задачи будем выполнять в следующие два этапа.