Курсовая работа: Решение обратных задач динамики

(1)

можно найти спектральную характеристику эталонного сигнала на выходе нелинейного элемента. Решая уравнение (1) относительно коэффициентов с использованием метода Гаусса-Ньютона получены следующие числовые значения коэффициентов:

. (2)

График соответствующего сигнала представлен на рисунке 4.

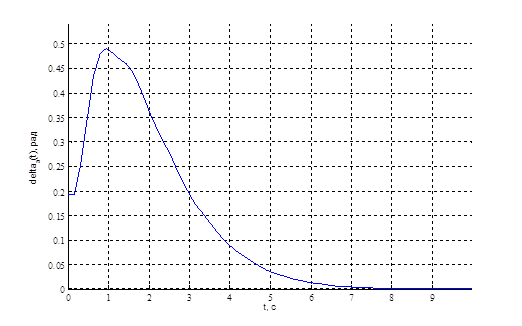
Рис. 4. График сигнала, который необходимо получить на выходе нелинейного элемента

Однако на выходе нелинейного элемента можно получить сигнал, представленный на рисунке 5 (ниже показаны первые пять элементов спектральной характеристики).

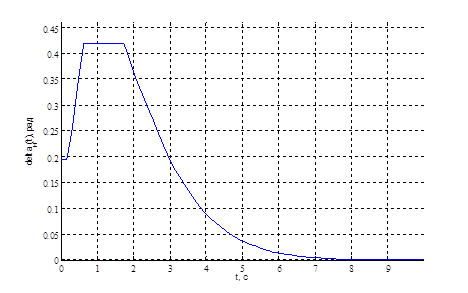
Рис. 5. Реальный сигнал на выходе нелинейного элемента

.

Тогда из (1) находим эталонный сигнал на выходе, который может обеспечить данная система (рис. 6). Его спектральная характеристика:

. (3)

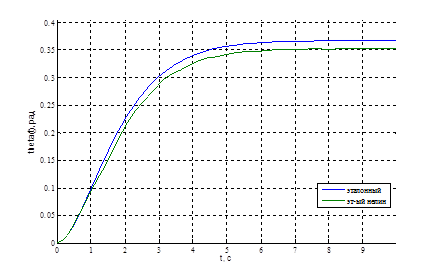
Рис. 6. Графики требуемого эталонного сигнала и эталонного сигнала, который можно получить

2. В результате решения предыдущего этапа найдены спектральные характеристики (3) эталонного выходного сигнала, который может обеспечить данная система, и (2) эталонного сигнала, которой необходимо получить на входе нелинейного элемента.

Далее искомый сигнал представим в виде

, (4)

где некоторая система линейно независимых функций.

В результате можно для спектральной характеристики сигнала на входе нелинейного элемента записать следующую зависимость.

, (5)

где – спектральная характеристика -го элемента системы . Поскольку известны спектральные характеристики эталонных сигналов и , то между левой и правой частями выражения (5) будет иметь место невязка

, (6)

зависящая от неизвестных коэффициентов , . Сформировав функционал

, (7)

исходную задачу синтеза входного сигнала можно свести к задаче поиска минимума функционала (7) на множестве допустимых значений коэффициентов , , т.е.

.

При решении задачи в качестве системы функций использовались экспоненциальные функции: . Минимум функционала (7) искался с использование алгоритма Нелдера-Мида (алгоритма безусловной минимизации). В качестве начальных значений искомых коэффициентов были приняты нулевые. При этом значение функционала (7):

.

Были получены следующие оптимальные значения искомых коэффициентов: